Question

某人需要补充维生素，现有甲、乙两种维生素胶囊，这两种胶囊都含有维生素A，C，D，E和最新发现的Z．甲种胶囊每粒含有维生素A，C，D，E，Z分别是1mg，1mg，4mg，4mg，5mg；乙种胶囊每粒含有维生素A，C，D，E，Z分别是3mg，2mg，1mg，3mg，2mg．此人每天摄入维生素A至多19mg，维生素C至多13mg，维生素D至多24mg，维生素E至少12mg．
（1）设该人每天服用甲种胶囊x粒，乙种胶囊y粒，为了能满足此人每天维生素的需要量，请写出x，y满足的不等关系．
（2）在（1）的条件下，他每天服用两种胶囊分别为多少时，可摄入最大量的维生素Z，且最大量为多少？

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：（1）直接由题意列出关于x，y的不等关系所组成的不等式组；
（2）由（1）中的不等式组作出可行域，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．

解答： 解：（1）由题意列关于x，y的不等式组

x+3y≤19 x+2y≤13 4x+y≤24 4x+3y≥12 x≥0 y≥0

；
（2）目标函数为：z=5x+2y．
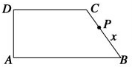
作出以上不等式组所表示的平面区域，即可行域如图．

作直线l：5x+2y=0，把直线向右上方平移，直线经过可行域上的点M时，z=5x+2y取得最大值．
解方程组

x+2y=13 4x+y=24

得M点坐标为（5，4），此时z=5×5+2×4=33（mg）．
答：每天服用5粒甲种胶囊和4粒乙种胶囊时，可摄入最大量的维生素Z为33mg．

点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．