Question

如图所示，直角梯形的下底AB=10，上底CD=7，sin∠ABC=

4

5

，设动点P由B点沿梯形的边经C、D运动到A．
（1）试求△PAB的面积S与点P所行路程x间的函数关系式S=f（x）；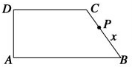
（2）画出S=f（x）的函数图象．

Answer 1

考点：函数解析式的求解及常用方法,函数的图象

专题：函数的性质及应用

分析：（1）由已知数据可求得BC=5，AD=4，分别求三角形的面积，综合可得解析式为S=f（x）=

4x，0≤x≤5 20，5＜x≤12 90-5x，12＜x≤18

；
（2）由S=f（x）的解析式可作函数图象．

解答： 解：（1）由已知数据可求得BC=5，AD=4，
∴当0≤x≤5时，S=

1

2

×10×

4

5

x=4x，
当5＜x≤12时，S=

1

2

×10×4=20，
当12＜x≤18时，

1

2

×10×（18-x）=90-5x，
综上可得S=f（x）=

4x，0≤x≤5 20，5＜x≤12 90-5x，12＜x≤18

；
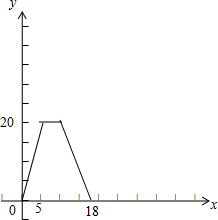
（2）S=f（x）的函数图象如下图所示：

点评：本题考查函数的解析式的求解以及函数的图象，涉及分类讨论的思想，属基础题．