题目内容
已知a1、x、y、a2成等差数列,b1、x、y、b2成等比数列,则
-2的取值范围是 .
| (a1+a2)2 |
| b1b2 |
考点:等差数列的性质,等比数列的性质
专题:等差数列与等比数列
分析:首先根据等比中项和等差中项得出a1+a2=x+y和b1b2=xy,再由均值不等式即可得出结果.
解答:
解:∵a1、x、y、a2成等差数列,∴a1+a2=x+y,
∵b1、x、y、b2成等比数列,∴b1b2=xy,
则
-2=
-2=
.
若xy>0,则
≥2;
若xy<0,则
≤-2.
故
-2的取值范围是(-∞,-2]∪[2,+∞).
故答案为(-∞,-2]∪[2,+∞).
∵b1、x、y、b2成等比数列,∴b1b2=xy,
则
| (a1+a2)2 |
| b1b2 |
| (x+y)2 |
| xy |
| x2+y2 |
| xy |
若xy>0,则
| x2+y2 |
| xy |
若xy<0,则
| x2+y2 |
| xy |
故
| (a1+a2)2 |
| b1b2 |
故答案为(-∞,-2]∪[2,+∞).
点评:此题考查了等比数列的性质和等差数列的性质,以及均值不等式的运用,属于基础题.

练习册系列答案
相关题目
给出如图的程序框图,那么输出的数是( )


| A、3 | B、4 | C、5 | D、6 |
已知f(x)=
若f(n-m)≤f(2m-n),则m+n的最小值是( )
|
| A、-5 | B、2 | C、5 | D、-2 |
在△ABC中,内角A、B、C所对的边分别是a、b、c,若c2=(a-b)2+6,c=
,则△ABC的面积是( )
| π |
| 2 |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、3
|
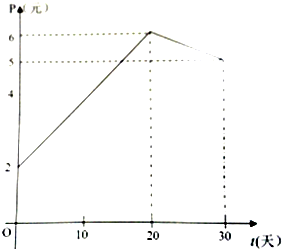 已知某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,p),点(t,p)落在图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示
已知某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对(t,p),点(t,p)落在图中的两条线段上,该股票在30天内(包括30天)的日交易量Q(万股)与时间t(天)的部分数据如下表所示