题目内容
8.某商人如果将进货单价为8元的商品按每件10元出售时,每天可销售100件,现他采用提高售价,减少进货量的办法增加利润,已知这种商品每件销售价提高1元,销售量就减少5件,问他将销售价每件定为多少元时,才能使得每天所赚的利润最大?最大利润是多少?分析 日利润=销售量×每件利润.每件利润为x-8元,销售量为100-5(x-10),据此得关系式.
解答 解:设每件x元出售,利润是y元.
y=(x-8)[100-(x-10)×5]=-5x2+190x-1200=-5(x-19)2+605(x>10),
故当x=19,即每件定为19元时,最大利润为605元.
点评 本题考查二次函数的应用,解题的关键是理解利润、销售量、每件利润之间的关系,学会构建二次函数解决在问题.

练习册系列答案
相关题目
5.四个人围坐在一张圆桌旁,每个人面前放着完全相同的硬币,所有人同时翻转自己的硬币.若硬币正面朝上,则这个人站起来; 若硬币正面朝下,则这个人继续坐着.那么,没有相邻的两个人站起来的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{7}{16}$ | C. | $\frac{1}{2}$ | D. | $\frac{9}{16}$ |
16.下列函数中,①y=sinx+tanx-x;②y=sin2x+cosx;③y=sin|x|;④$y=3sin2({x+\frac{π}{4}})$,属于偶函数的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.下列给出的函数中,既不是奇函数也不是偶函数的是( )
| A. | $y=\frac{2}{x}$ | B. | y=x3 | C. | y=-x2 | D. | $y=\sqrt{x}$ |
13.已知向$\overrightarrow{a}$=(1,n),$\overrightarrow{b}$=(-1,n),$\overrightarrow{a}$垂直于$\overrightarrow{b}$,则|$\overrightarrow{a}$|=( )
| A. | 1 | B. | $\frac{\sqrt{6}}{2}$ | C. | 4 | D. | $\sqrt{2}$ |
20.下列各组函数表示相等函数的是( )
| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
18.设△ABC的内角A,B,C所对的边分别为a,b,c若cos2$\frac{B}{2}=\frac{a+c}{2c}$,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不确定 |
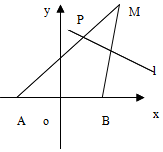 已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.
已知A点坐标为$(-2\sqrt{3},0)$,B点坐标为$(2\sqrt{3},0)$,且动点M到A点的距离是8,线段MB的垂直平分线l交线段MA于点P.