题目内容
16.下列函数中,①y=sinx+tanx-x;②y=sin2x+cosx;③y=sin|x|;④$y=3sin2({x+\frac{π}{4}})$,属于偶函数的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 ①,定义域为{x|x≠kπ+$\frac{π}{2}$},关于原点对称,且f(-x)=-f(x),故①为奇函数;
②③,定义域为R关于原点对称,且f(-x)=f(x),故②为偶函数;
④,$y=3sin2({x+\frac{π}{4}})$=3sin(2x+$\frac{π}{2}$)=3cos2x,满足定义域为R关于原点对称\f(-x)=f(x),故④为偶函数,
解答 解:对于①,定义域为{x|x≠kπ+$\frac{π}{2}$},关于原点对称,且f(-x)=-f(x),故①为奇函数,排除①;
对于②③,定义域为R关于原点对称,且f(-x)=f(x),故②为偶函数,故②③满足条件;
对于④,$y=3sin2({x+\frac{π}{4}})$=3sin(2x+$\frac{π}{2}$)=3cos2x,满足定义域为R关于原点对称\f(-x)=f(x),故④为偶函数,满足条件,
故选:D
点评 本题考查奇偶函数的定义,考查学生分析解决问题的能力,比较基础.

练习册系列答案
相关题目
7.已知一个几何体的三视图如图所示,则该几何体的体积是( )
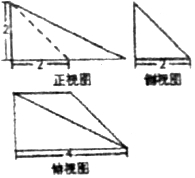

| A. | 2 | B. | 4 | C. | 6 | D. | 1 |
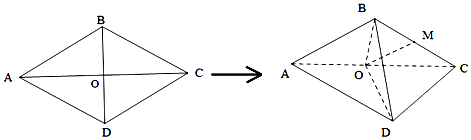
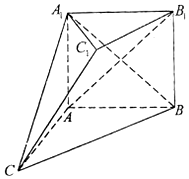 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC