题目内容
17.已知实数x,y满足x2+y2-4x-6y+12=0,则x-y的最大值为1+$\sqrt{2}$.分析 由x2+y2-4x-6y+12=0,可得(x-2)2+(y-3)2=1,此方程表示圆心为C(2,3),半径为1的圆.令x-y=t,利用点到直线的距离公式可得$\frac{|1-t|}{\sqrt{2}}$≤1,解出即可.
解答 解:由x2+y2-4x-6y+12=0,∴(x-2)2+(y-3)2=1,
∴圆心为C(2,3),半径为1.
令x-y=t,则$\frac{|1-t|}{\sqrt{2}}$≤1,
解得1-$\sqrt{2}$≤t≤1+$\sqrt{2}$,
∴x-y的最大值是1+$\sqrt{2}$.
故答案为1+$\sqrt{2}$.
点评 本题考查了直线与圆的位置关系、点到直线的距离公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知一个几何体的三视图如图所示,则该几何体的体积是( )
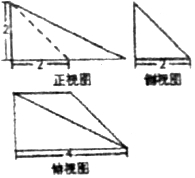

| A. | 2 | B. | 4 | C. | 6 | D. | 1 |
12.在△ABC中,“sinA=sinB”是“A=B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.若x>0,y>0,且$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$,则xy有( )
| A. | 最大值16 | B. | 最小值$\frac{1}{16}$ | C. | 最小值16 | D. | 最小值$\frac{1}{2}$ |
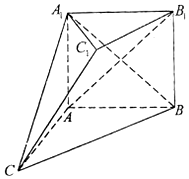 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC