题目内容
20.下列各组函数表示相等函数的是( )| A. | $f(x)={({\sqrt{x}})^2}$和$g(x)=\sqrt{x^2}$ | B. | $f(x)={({\root{3}{x+1}})^3}$和$g(x)=\root{3}{{{{({x+1})}^3}}}$ | ||
| C. | f(x)=2lgx和g(x)=lg x2 | D. | f(x)=ln x-ln(x-1)和$g(x)=ln\frac{x}{x-1}$ |
分析 分别求出各个选项中函数的定义域,或化简解析式,由函数相等的定义进行判断即可.
解答 解:A、$f(x)={(\sqrt{x})}^{2}$的定义域是(0,+∞),$g(x)=\sqrt{{x}^{2}}$的定义域是R,
即函数f(x)、g(x)不是相等函数,A不正确;
B、$f(x)={(\root{3}{x+1})}^{3}$=x+1,且x∈R,$g(x)=\root{3}{{(x+1)}^{3}}$=x+1,且x∈R,
即函数f(x)、g(x)是相等函数,B正确;
C、f(x)=2lgx的定义域是(0,+∞),g(x)=lg x2的定义域是{x|x≠0},
即函数f(x)、g(x)不是相等函数,C不正确;
D、由$\left\{\begin{array}{l}{x>0}\\{x-1>0}\end{array}\right.$得x>1,函数f(x)的定义域是(0,+∞),
由$\frac{x}{x-1}>0$得x(x-1)>0,解得x>1或x<0,函数g(x)的定义域是(∞,0)∪(1,+∞),
即函数f(x)、g(x)不是相等函数,D不正确,
故选:B.
点评 本题考查函数相等的判断方法:定义法,以及函数定义域的求解,属于基础题.

练习册系列答案
相关题目
10.设f(x)是定义在R上的函数,其导函数为f′(x),若f(x)+f′(x)>1,f(0)=2017,则不等式exf(x)>ex+2016(其中e为自然对数的底数)的解集为( )
| A. | (-∞,0)∪(0,+∞) | B. | (0,+∞) | C. | (2016,+∞) | D. | (-∞,0)∪(2016,+∞) |
12.在△ABC中,“sinA=sinB”是“A=B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.若x>0,y>0,且$\frac{1}{x}+\frac{1}{y}=\frac{1}{2}$,则xy有( )
| A. | 最大值16 | B. | 最小值$\frac{1}{16}$ | C. | 最小值16 | D. | 最小值$\frac{1}{2}$ |
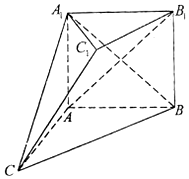 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B=BC,B1C1∥BC,B1C1=$\frac{1}{2}$BC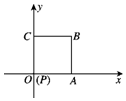 如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.
如图放置的边长为2的正方形PABC沿x轴正半轴滚动.设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为8;y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为4π+4.