题目内容
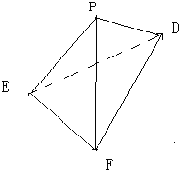 三棱锥P-DEF中,顶点P在平面DEF上的射影为O.
三棱锥P-DEF中,顶点P在平面DEF上的射影为O.(1)如果PE=PF=PD,证明O是三角形DEF的外心(外接圆的圆心)
(2)如果PE=PF=1,PD=2,EF=
| 2 |
| 5 |
考点:直线与平面垂直的性质,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)连接OD、OE、OF,由PD=PE=PF可得:Rt△PDO≌Rt△PEO≌Rt△PFO,进而得到:OD=OE=OF,即O是三角形DEF的外心(外接圆的圆心)
(2)如果PE=PF=1,PD=2,EF=
,DE=DF=
,由勾股定理可得:△PEF、PDF、PED都是直角三角形,由线面垂直的判定定理和性质定理,可证得DF⊥EO,EF⊥DO,DE⊥FO,即O是三角形DEF的垂心(三条高的交点).
(2)如果PE=PF=1,PD=2,EF=
| 2 |
| 5 |
解答:
证明:(1)过P作PO垂直于平面DEF,O为垂足,
连接OD、OE、OF,
∵PD=PE=PF
∴Rt△PDO≌Rt△PEO≌Rt△PFO,
∴OD=OE=OF,
故O为三角形DEF的外心.(4分)
(2)过P作PO垂直于平面DEF,O为垂足,
∵PE=PF=1,EF=
,DE=DF=
,PD=2,
∴△PEF、PDF、PED都是直角三角形.…(1分)
⇒PE⊥平面PDF…(3分)
⇒
⇒PE⊥DF…(1分)
又
⇒PO⊥DF,
∵PE∩PO=P,PE,PO?平面PEO,
∴DF⊥平面PEO,
又∵EO?平面PEO,
∴DF⊥EO,
同理可得:EF⊥DO,DE⊥FO,
即O是三角形DEF的垂心.
连接OD、OE、OF,
∵PD=PE=PF
∴Rt△PDO≌Rt△PEO≌Rt△PFO,
∴OD=OE=OF,
故O为三角形DEF的外心.(4分)
(2)过P作PO垂直于平面DEF,O为垂足,
∵PE=PF=1,EF=
| 2 |
| 5 |
∴△PEF、PDF、PED都是直角三角形.…(1分)
|
⇒
|
又
|
∵PE∩PO=P,PE,PO?平面PEO,
∴DF⊥平面PEO,
又∵EO?平面PEO,
∴DF⊥EO,
同理可得:EF⊥DO,DE⊥FO,
即O是三角形DEF的垂心.
点评:本题考查的知识点是直线与平面垂直的判定,直线与平面垂直的性质,勾股定理,三角形的四心,难度不大,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
已知sinα=
,则sin(π-α)=( )
| 1 |
| 3 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
参数方程
(θ为参数)化为普通方程是( )
|
| A、2x-y+1=0 |
| B、2x+y-1=0 |
| C、2x-y+1=0,x∈[0,1] |
| D、2x+y-1=0,x∈[0,1] |

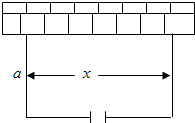 某动物园要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).
某动物园要围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元).