题目内容
已知函数f(x)=
x2+alnx.
(1)若a=-1,求函数f(x)的极值,并指出极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在g(x)=
x3的图象下方.
| 1 |
| 2 |
(1)若a=-1,求函数f(x)的极值,并指出极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最值;
(3)若a=1,求证:在区间[1,+∞)上,函数f(x)的图象在g(x)=
| 2 |
| 3 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:(1)代入a=-1,从而化简f(x)并求其定义域,再求导判断函数的单调性及极值即可;
(2)代入a=1,从而化简f(x)并求其定义域,再求导判断函数的单调性及求函数的最值;
(3)代入a=1,令F(x)=g(x)-f(x)=
x3-
x2-lnx,从而化在区间[1,+∞)上,函数f(x)的图象在g(x)=
x3的图象下方为F(x)>0在[1,+∞)上恒成立,再化为函数的最值问题即可.
(2)代入a=1,从而化简f(x)并求其定义域,再求导判断函数的单调性及求函数的最值;
(3)代入a=1,令F(x)=g(x)-f(x)=
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
解答:
解:(1)当a=-1时,f(x)=
x2-lnx的定义域为(0,+∞),
f′(x)=x-
=
;
故f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
故f(x)在x=1处取得极小值f(1)=
;
(2)当a=1时,f(x)=
x2+lnx的定义域为(0,+∞),
f′(x)=x+
>0;
故f(x)在[1,e]上是增函数,
故fmin(x)=f(1)=
,fmax(x)=f(e)=
e2+1;
(3)证明:令F(x)=g(x)-f(x)=
x3-
x2-lnx;
则F′(x)=2x2-x-
=
,
∵x∈[1,+∞),
∴F′(x)=
≥0,
∴F(x)在[1,+∞)上是增函数,
故F(x)≥F(1)=
-
=
>0;
故在区间[1,+∞)上,函数f(x)的图象在g(x)=
x3的图象下方.
| 1 |
| 2 |
f′(x)=x-
| 1 |
| x |
| (x-1)(x+1) |
| x |
故f(x)在(0,1)上是减函数,在(1,+∞)上是增函数,
故f(x)在x=1处取得极小值f(1)=
| 1 |
| 2 |
(2)当a=1时,f(x)=
| 1 |
| 2 |
f′(x)=x+
| 1 |
| x |
故f(x)在[1,e]上是增函数,
故fmin(x)=f(1)=
| 1 |
| 2 |
| 1 |
| 2 |
(3)证明:令F(x)=g(x)-f(x)=
| 2 |
| 3 |
| 1 |
| 2 |
则F′(x)=2x2-x-
| 1 |
| x |
| (x-1)(2x2+x+1) |
| x |
∵x∈[1,+∞),
∴F′(x)=
| (x-1)(2x2+x+1) |
| x |
∴F(x)在[1,+∞)上是增函数,
故F(x)≥F(1)=
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
故在区间[1,+∞)上,函数f(x)的图象在g(x)=
| 2 |
| 3 |
点评:本题考查了导数的综合应用,同时考查了函数的图象与函数的性质的关系及恒成立问题,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,点O为底面ABCD的中心,P为棱A1B1上任一点,则异面直线OP与AM所成的角的大小为( )
| A、30° | B、60° |
| C、90° | D、120° |
方程x+y+z=10的正整数解的个数( )
A、
| ||
B、
| ||
C、
| ||
D、
|
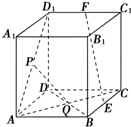 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、P、Q分别是BC、C1D1、AD1、BD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、P、Q分别是BC、C1D1、AD1、BD的中点.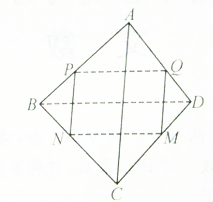 如图,在四面体ABCD中,截面PQMN是平行四边形.
如图,在四面体ABCD中,截面PQMN是平行四边形.