题目内容
函数y=sin（arcsinx）+
的值域是 ．
| 3 |
| sin(arcsinx) |
考点：三角函数中的恒等变换应用
专题：函数的性质及应用,三角函数的求值
分析：首先根据函数的定义域求出三角函数的单调性，进一步利用函数的奇偶性确定函数的最值．
解答：
解：函数y=f（x）=sin（arcsinx）+
的定义域为：[-1，0）∪（0，1]
由于：①函数的定义域关于原点对称
②f（-x）=-f（x）
所以函数f（x）为奇函数．
所以：函数的图象关于原点对称．
③当x∈（0，1]
则：f（x）=sin（arcsinx）+
为单调递减函数，
则当x=1时，函数有最小值4，
④当x∈[-1，0）则：f（x）=sin（arcsinx）+
为单调递减函数，
所以当x=-1时，函数有最大值-4．
函数的值域为：（-∞，-4]∪[4，+∞）
故答案为：（-∞，-4]∪[4，+∞）
| 3 |
| sin(arcsinx) |
由于：①函数的定义域关于原点对称
②f（-x）=-f（x）
所以函数f（x）为奇函数．
所以：函数的图象关于原点对称．
③当x∈（0，1]
则：f（x）=sin（arcsinx）+
| 3 |
| sin(arcsinx) |
则当x=1时，函数有最小值4，
④当x∈[-1，0）则：f（x）=sin（arcsinx）+
| 3 |
| sin(arcsinx) |
所以当x=-1时，函数有最大值-4．
函数的值域为：（-∞，-4]∪[4，+∞）
故答案为：（-∞，-4]∪[4，+∞）
点评：本题考查的知识要点：反三角函数的值域的应用，函数性质的应用，属于基础题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
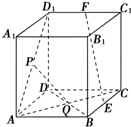如图，在棱长为a的正方体ABCD-A1B1C1D1中，E、F、P、Q分别是BC、C1D1、AD1、BD的中点．方程x+y+z=10的正整数解的个数（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|