题目内容
在长方体ABCD-A1B1C1D1中,其中ABCD是正方形,AA1>AB.设点A到直线B1D的距离和到平面DCB1A1的距离分别为d1,d2,则
的取值范围是 .
| d1 |
| d2 |
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:设AB=a,AA1=b(b>a),利用长方体中的垂直关系和面积相等求出d1,连接A1D、过A作AE⊥A1D,利用长方体中的垂直关系、线面垂直的判定定理和定义,得到d2=AE,利用面积相等求出d2,化简
后设t=
,求出0<t<1,化简后利用基本不等式和函数的单调性求出
的范围.
| d1 |
| d2 |
| a2 |
| b2 |
| d1 |
| d2 |
解答:
解:设AB=a,AA1=b,由AA1>AB得b>a,
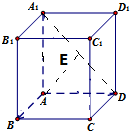 所以点A到直线B1D的距离d1=
所以点A到直线B1D的距离d1=
=
,
连接A1D,过A作AE⊥A1D,
由CD⊥平面ADD1A1得,CD⊥AE,又AE⊥A1B,则AE⊥平面DCB1A1,
所以AE为点A到平面DCB1A1的距离,
则d2=AE=
=
,
所以
=
=
,上式分子分母同除以b2得,
=
,
设t=
,则0<t<1,代入上式可得
=
,
设y=
=
=
=
≥
=1,
当且仅当t+
=
时取等号,此时t=0,
因为0<t<1,函数y在(0,1)上是增函数,当t=1时,y=
=
,
所以1<y<
,
∈(1,
),
故答案为:(1,
).
 所以点A到直线B1D的距离d1=
所以点A到直线B1D的距离d1=| AD•AB1 |
| B1D |
a
| ||
|
连接A1D,过A作AE⊥A1D,
由CD⊥平面ADD1A1得,CD⊥AE,又AE⊥A1B,则AE⊥平面DCB1A1,
所以AE为点A到平面DCB1A1的距离,
则d2=AE=
| AD•AA1 |
| A1D |
| ab | ||
|
所以
| d1 |
| d2 |
| a(a2+b2) | ||
ab
|
| a2+b2 | ||
b
|
| d1 |
| d2 |
| ||||
|
设t=
| a2 |
| b2 |
| d1 |
| d2 |
| t+1 | ||
|
设y=
| t+1 | ||
|
|
|
|
|
当且仅当t+
| 1 |
| 2 |
| 1 | ||
4(t+
|
因为0<t<1,函数y在(0,1)上是增函数,当t=1时,y=
| 2 | ||
|
2
| ||
| 3 |
所以1<y<
2
| ||
| 3 |
| d1 |
| d2 |
2
| ||
| 3 |
故答案为:(1,
2
| ||
| 3 |
点评:本题的考点是点、线、面间的距离计算,线面垂直的判定定理和定义,面积相等法求距离,关键是利用长方体的几何特征寻找表示点面距离的线段,再转化为函数关系利用函数的单调性、基本不等式求最值,注意换元法的应用以及变量的范围确定,属于难题.

练习册系列答案
相关题目
方程x+y+z=10的正整数解的个数( )
A、
| ||
B、
| ||
C、
| ||
D、
|
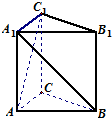 直三棱柱ABC-A1B1C1中,AC=AB=AA1,且异面直线AC1与A1B所成的角为60°,则∠CAB等于
直三棱柱ABC-A1B1C1中,AC=AB=AA1,且异面直线AC1与A1B所成的角为60°,则∠CAB等于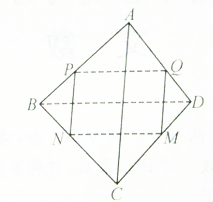 如图,在四面体ABCD中,截面PQMN是平行四边形.
如图,在四面体ABCD中,截面PQMN是平行四边形.