题目内容
6.设函数f(x)=|x-c|.(Ⅰ)求证:$f(x)+f(-\frac{1}{x})≥2$;
(Ⅱ)若c>2,不等式$|{f({\frac{1}{2}x+c})-\frac{1}{2}f(x)}|≤1$的解集为{x|1≤x≤3},求c的值.
分析 (Ⅰ)根据绝对值的性证明即可;(Ⅱ)求出g(x)的分段函数的形式,得到关于c的方程组,解出即可.
解答 (Ⅰ)证明:$f(x)+f(-\frac{1}{x})=|{x-c}|+|{-\frac{1}{x}-c}|=|{x-c}|+|{\frac{1}{x}+c}|$$≥|{(x-c)+(\frac{1}{x}+c)}|=|{x+\frac{1}{x}}|=|x|+\frac{1}{|x|}≥2\sqrt{|x|+\frac{1}{|x|}}=2$;
(Ⅱ)解:$g(x)=f(\frac{1}{2}x+c)-\frac{1}{2}f(x)=|{\frac{1}{2}x+c-c}|-\frac{1}{2}|{x-c}|=\frac{1}{2}|x|-\frac{1}{2}|{x-c}|$,
则$g(x)=\left\{\begin{array}{l}-\frac{c}{2},x≤0\\ x-\frac{c}{2},0<x<c\\ \frac{c}{2},x≥c\end{array}\right.$,
由|g(x)|≤1时,又c>2,所以$|{x-\frac{c}{2}}|≤1$,
即$-1≤x-\frac{1}{2}≤1$,所以$\left\{\begin{array}{l}1+\frac{c}{2}=3\\-1+\frac{c}{2}=1\end{array}\right.$,
所以c=4.
点评 本题考查了绝对值不等式问题,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
18.如果执行如所示的程序框图,那么输出的S=( )


| A. | 119 | B. | 600 | C. | 719 | D. | 4949 |
15. 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
测试成绩(单位:次/分钟)如表:
(Ⅰ)补全茎叶图并指出乙队测试成绩的中位数和众数;
(Ⅱ)试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析.
 为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,
为迎接即将举行的集体跳绳比赛,高一年级对甲、乙两个代表队各进行了6轮测试,测试成绩(单位:次/分钟)如表:
| 轮次 | 一 | 二 | 三 | 四 | 五 | 六 |
| 甲 | 73 | 66 | 82 | 72 | 63 | 76 |
| 乙 | 83 | 75 | 62 | 69 | 75 | 68 |
(Ⅱ)试用统计学中的平均数、方差知识对甲乙两个代表队的测试成绩进行分析.
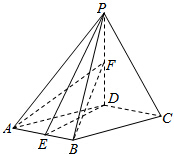 已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.
已知四棱锥P-ABCD,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E为AB中点,点F为PD中点.