题目内容
16.若函数f(x)=$\left\{\begin{array}{l}{lnx,(x>0)}\\{{e}^{x+1}-2,(x≤0)}\end{array}\right.$,则f(f($\frac{1}{e}$))=( )| A. | -1 | B. | 0 | C. | 1 | D. | 3 |
分析 利用分段函数直接求解函数值即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{lnx,(x>0)}\\{{e}^{x+1}-2,(x≤0)}\end{array}\right.$,
则f(f($\frac{1}{e}$))=f(ln$\frac{1}{e}$)=f(-1)=e0-2=-1.
故选:A.
点评 本题考查分段函数的应用,函数值的求法,对数运算法则的应用,是基础题

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案
相关题目
7.设集合S={1,2,…,2016},若X是S的子集,把X中所有元素之和称为X的“容量”,(规定空集容量为0),若X的容量为奇(偶)数,则称X为S的奇(偶)子集,记S的奇子集个数为m,偶子集个数为n,则m,n之间的关系为( )
| A. | m=n | B. | m>n | C. | m<n | D. | 无法确定 |
4.阅读如图所示的程序框图,运行相应的程序,若判断框内是n≤6,则输出的S为( )
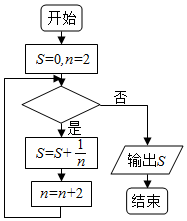

| A. | $\frac{3}{4}$ | B. | $\frac{25}{24}$ | C. | $\frac{11}{12}$ | D. | $\frac{5}{6}$ |
1.某几何体的三视图如图所示,则该几何体的体积为( )
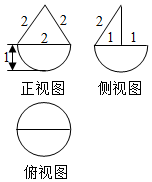

| A. | $\frac{4+\sqrt{3}}{3}$π | B. | $\frac{4+\sqrt{3}}{6}$π | C. | $\frac{2+\sqrt{3}}{3}$π | D. | $\frac{5π}{6}$ |
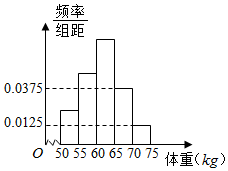 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为10,则抽取的学生人数为40.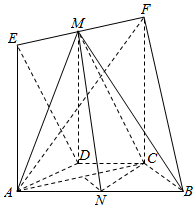 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.