题目内容

双曲线
x2
5
-
y2
4
=1的右焦点的坐标为
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据双曲线的方程和性质即可得到结论．
解答： 解：由双曲线的方程可知，a2=5，b2=4，
则c2=a2+b2=9，即c=3，
故双曲线的右焦点的坐标为：（3，0），
故答案为：（3，0）．
点评：本题主要考查双曲线的性质和方程，根据a，b，c之间的关系是解决本题的关键．
练习册系列答案
相关题目
方程f（x）=x的根称为f（x）的不动点，若函数f（x）=
x
a(x+2)
有唯一不动点，且x1=2，xn+1=
1
f(
2
xn
)
（n∈N+），则log
1
2
（x2014-1）=（　　）
A、2014B、2013
C、1D、0
如图，电路中共有7个电阻与一个电灯A，若灯A不亮，分析因电阻断路的可能性共有
 
种
直角坐标系xOy中，以原点为极点，x轴的正半轴为极轴建立极坐标系，设点A，B分别在曲线C1：
x=3+cost
y=4+sint
（t为参数）和曲线C2：ρ=1上，当|AB|长取得最小值时，求线段AB的垂直平分线的极坐标方程．
一个圆锥的侧面展开图是一个半径为6的半圆，则这个圆锥的体积等于
 
．
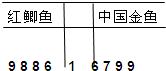已知某人工养殖观赏鱼池塘中养殖着大量的红鲫鱼与中国金鱼．为了估计池塘中这两种鱼的数量，养殖人员从水库中捕出了红鲫鱼与中国金鱼各1000只，给每只鱼作上不影响其存活的记号，然后放回池塘，经过一定时间，再每次从池塘中随机地捕出1000只鱼，分类记录下其中有记号的鱼的数目，随即将它们放回池塘中．这样的记录作了10次．并将记录获取的数据做成以下的茎叶图，
（Ⅰ）根据茎叶图计算有记号的红鲫鱼与中国金鱼数目的平均数，并估计池塘中的红鲫鱼与中国金鱼的数量；
（Ⅱ）假设随机地从池塘逐只有放回地捕出5只鱼中的红鲫鱼的数目为ξ，求ξ的分布列与数学期望．
下列函数中，最小正周期为π，且图象关于直线x=-
π
3
对称的是（　　）
A、y=cos(2x-
π
3
)
B、y=sin(2x-
π
6
)
C、y=sin(2x+
π
6
)
D、y=cos(
x
2
+
π
6
)
两个非零向量
a
，
b
垂直的充要条件是（　　）
A、|
a
+
b
|=|
a
-
b
|
B、
a
•（
a
-
b
）=0
C、
a
•
b
=|
a
||
b
|
D、（
a
+
b
）（
a
-
b
）=0
E、
a
•（
a
-
b
）=0，得到
a
⊥
a
-
b
，但是
a
，
b
的数量积不一定为0，所以两根向量不一定垂直；
F、（
a
+
b
）（
a
-
b
）=0，展开得
a
2=
b
2，得到向量的长度相等，但是位置不一定垂直；
已知函数f（x）=x2+ax+b满足f（1）=f（3）=0，则f（2）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网