题目内容
9.某个命题和正整数n有关,如果当n=k,k为正整数时命题成立,那么可推得当n=k+1时,命题也成立.现已知当n=7时命题不成立,那么可以推得( )| A. | 当n=6时该命题不成立 | B. | 当n=6时该命题成立 | ||
| C. | 当n=8时该命题不成立 | D. | 当n=8时该命题成立 |
分析 利用命题与逆否命题的真假性相同,结合数学归纳法推出结果即可.
解答 解:命题与逆否命题的真假性相同,所以当n=k,k为正整数时命题成立,那么可推得当n=k+1时,命题也成立.现已知当n=7时命题不成立,那么可以推得当n=6时该命题不成立.
故选:A.
点评 本题考查数学归纳法的应用,逆否命题与原命题的真假关系,考查转化思想.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
19.曲线y=3sin2x图象上所有点的横坐标伸长为原来的2倍,纵坐标变为原来的$\frac{1}{3}$倍,所得图象对应的解析式为( )
| A. | y=9sin4x | B. | y=sin4x | C. | y=9sinx | D. | y=sinx |
17.在函数 ①y=cos|2x|,②y=|cosx|,③$y=|sin(2x+\frac{π}{2})|$,④y=tan|x|中,最小正周期为π的所有偶 函数为( )
| A. | ①② | B. | ①②③ | C. | ②④ | D. | ①③ |
4.命题“x>0,总有(x+1)ex>1”的否定是( )
| A. | “x>0,使得(x+1)ex>1” | B. | “x>0,总有(x+1)ex≥1” | ||
| C. | “x>0,使得(x+1)ex≤1” | D. | x>0,总有(x+1)ex<1” |
14.已知某帆船中心比赛场馆区的海面上每天海浪高度y(米)可看作是时间t(0≤t≤24,单位:小时)的函数,记作y=f(t),经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b,下表是某日各时的浪高数据:
则最能近似地表示表中数据间对应关系的函数是( )
| t/时 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/米 | 2 | $\frac{3}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{3}{2}$ | 0.99 | $\frac{3}{2}$ | 2 |
| A. | y=$\frac{1}{2}$cos$\frac{π}{6}$t+1 | B. | y=$\frac{1}{2}$cos$\frac{π}{6}$t+$\frac{3}{2}$ | C. | y=2cos$\frac{π}{6}$t+$\frac{3}{2}$ | D. | y=$\frac{1}{2}$cos6πt+$\frac{3}{2}$ |
18.某班一个学习小组在一次数学实践活动中,测得一组数据共5个,如表
若x1+x2+x3+x4=10,计算得回归方程为$\stackrel{∧}{y}$=2.5x-2.3,则n的值为( )
| x | x1 | x2 | x3 | x4 | 5 |
| y | 2.5 | 4.6 | 5.4 | n | 7.5 |
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
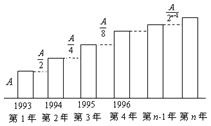 甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示:
甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示: