题目内容
4．命题“x＞0，总有（x+1）ex＞1”的否定是（ ）| A． | “x＞0，使得（x+1）ex＞1” | B． | “x＞0，总有（x+1）ex≥1” | ||
| C． | “x＞0，使得（x+1）ex≤1” | D． | x＞0，总有（x+1）ex＜1” |
分析 直接利用全称命题的否定是特称命题写出结果即可．
解答 解：因为全称命题的否定是特称命题，
所以命题“x＞0，总有（x+1）ex＞1”的否定是：x＞0，使得（x+1）ex≤1．
故选：C
点评 本题考查命题的否定，特称命题与全称命题的否定关系．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．
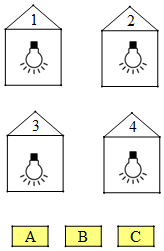如图，A，B，C三个开关控制着1，2，3，4号四盏灯．若开关A控制着2，3，4号灯（即按一下开关A，2，3，4号灯亮，再按一下开关A，2，3，4号灯熄灭），同样，开关B控制着1，3，4号灯，开关C控制着1，2，4号灯．开始时，四盏灯都亮着，那么下列说法正确的是（ ）
如图，A，B，C三个开关控制着1，2，3，4号四盏灯．若开关A控制着2，3，4号灯（即按一下开关A，2，3，4号灯亮，再按一下开关A，2，3，4号灯熄灭），同样，开关B控制着1，3，4号灯，开关C控制着1，2，4号灯．开始时，四盏灯都亮着，那么下列说法正确的是（ ）| A． | 只需要按开关A，C可以将四盏灯全部熄灭 | |
| B． | 只需要按开关B，C可以将四盏灯全部熄灭 | |
| C． | 按开关A，B，C可以将四盏灯全部熄灭 | |
| D． | 按开关A，B，C无法将四盏灯全部熄灭 |
9．某个命题和正整数n有关，如果当n=k，k为正整数时命题成立，那么可推得当n=k+1时，命题也成立．现已知当n=7时命题不成立，那么可以推得（ ）
| A． | 当n=6时该命题不成立 | B． | 当n=6时该命题成立 | ||
| C． | 当n=8时该命题不成立 | D． | 当n=8时该命题成立 |
16．已知点P（x，y）的坐标满足x2+y2-2y=0，则$u=\frac{y+1}{x}$的取值范围是（ ）
| A． | $-\sqrt{3}≤u≤\sqrt{3}$ | B． | $u≥\sqrt{3}$或$u≤-\sqrt{3}$ | C． | $-\frac{{\sqrt{3}}}{3}≤u≤\frac{{\sqrt{3}}}{3}$ | D． | $u≥\frac{{\sqrt{3}}}{3}$或$u≤-\frac{{\sqrt{3}}}{3}$ |
13．某商品的销售量y（件）与销售价格x（元/件）存在线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为$\widehat{y}$=-10x+200，则下列结论正确的是（ ）
| A． | y与x成正线性相关关系 | |
| B． | 当商品销售价格提高1元时，商品的销售量减少200件 | |
| C． | 当销售价格为10元/件时，销售量为100件 | |
| D． | 当销售价格为10元/件时，销售量为100件左右 |