题目内容
20.已知函数f(x)=ln(1+x)-$\frac{ax}{x+1}$(a>0).(1)若x=1是函数f(x)的一个极值点,求a的值;
(2)若f(x)≥0在[0,+∞)上恒成立,求a的取值范围;
(3)证明:${(\frac{2017}{2016})^{2017}}$>e(e为自然对数的底数).
分析 (1)求出函数的导数,得到关于a的方程,解出即可;
(2)问题转化为f(x)min≥0,根据函数的单调性,通过讨论a的范围求出a的具体范围即可;
(3)不等式两边取对数,得到ln(1+$\frac{1}{1+2016}$)-$\frac{1}{1+2016}$>0,结合函数的单调性证明即可.
解答 解:(1)∵f(x)=ln(1+x)-$\frac{ax}{x+1}$(a>0),
∴f′(x)=$\frac{x+1-a}{{(x+1)}^{2}}$,
∵x=1是函数f(x)的一个极值点,
f′(1)=0即a=2;
(2)∵f(x)≥0在[0,+∞)上恒成立,∴f(x)min≥0,
当0<a≤1时,f′(x)≥0在[0,+∞)上恒成立,
即f(x)在[0,+∞)上为增函数,
∴f(x)min=f(0)=0成立,即0<a≤1,
当a>1时,令f′(x)≥0,则x>a-1,
令f′(x)<0,则0≤x<a-1,
即f(x)在[0,a-1)上为减函数,在(a-1,+∞)上为增函数,
∴f(x)min=f(a-1)≥0,又f(0)=0>f(a-1),则矛盾.
综上,a的取值范围为(0,1].
(3)两边取自然对数得,2017×ln$\frac{2017}{2016}$>1?ln $\frac{2017}{2016}$>$\frac{1}{2017}$,
?ln$\frac{2017}{2016}$-$\frac{1}{2017}$>0?ln(1+$\frac{1}{2016}$)-$\frac{1}{1+2016}$>0,
由(2)知a=1时,f(x)=ln(1+x)-$\frac{x}{x+1}$在[0,+∞)单调递增,
又 $\frac{1}{1+2016}$>0,f(0)=0,
∴f( $\frac{1}{2016}$)=ln $\frac{1}{1+2016}$-$\frac{1}{1+2016}$>f(0)=0,
故${(\frac{2017}{2016})^{2017}}$>e成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.

| A. | [6,+∞) | B. | (-∞,-6]∪[6,+∞) | C. | (6,+∞) | D. | (-6,6) |
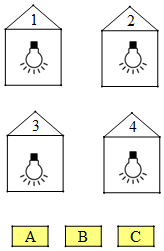 如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )| A. | 只需要按开关A,C可以将四盏灯全部熄灭 | |
| B. | 只需要按开关B,C可以将四盏灯全部熄灭 | |
| C. | 按开关A,B,C可以将四盏灯全部熄灭 | |
| D. | 按开关A,B,C无法将四盏灯全部熄灭 |
| A. | 当n=6时该命题不成立 | B. | 当n=6时该命题成立 | ||
| C. | 当n=8时该命题不成立 | D. | 当n=8时该命题成立 |
| A. | (-$\frac{3}{2}$,-$\frac{18}{5}$) | B. | ($\frac{4}{3}$,-$\frac{4}{3}$) | C. | (-2,-4) | D. | ($\frac{3}{2}$,-$\frac{6}{5}$) |
 如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )