题目内容
1.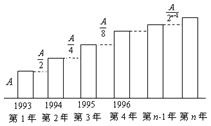 甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示:
甲、乙两家网络公司,1993年的市场占有率均为A,根据市场分析与预测,甲、乙公司自1993年起逐年的市场占有率都有所增加,甲公司自1993年起逐年的市场占有率都比前一年多$\frac{A}{2}$,乙公司自1993年起逐年的市场占有率如图所示:(I)求甲、乙公司第n年市场占有率的表达式;
(II)根据甲、乙两家公司所在地的市场规律,如果某公司的市场占有率不足另一公司市场占有率的20%,则该公司将被另一公司兼并,经计算,2012年之前,不会出现兼并局面,试问2012年是否会出现兼并局面,并说明理由.
分析 (I)由{an}是以a1=A为首项,以$d=\frac{A}{2}$为公差的等差数列,根据等差数列前n项和公式即可求得an,{bn}是以a2=A为首项,以$\frac{A}{2}$为公比的等比数列,利用等比数列前n项和公式即可求得bn;
(II)由${a_{20}}=\frac{A}{2}×20+\frac{A}{2}=\frac{21}{2}A>10A$,则$\frac{{{b_{20}}}}{{{a_{20}}}}<\frac{2A}{10A}=20%$,即b20<20%•a20,则2012年会出现乙公司被甲公司兼并的局面.
解答 解:(I)设甲公司第n年市场占有率为an,
依题意,{an}是以a1=A为首项,以$d=\frac{A}{2}$为公差的等差数列.(2分)
∴${a_n}=A+(n-1)•\frac{A}{2}=\frac{A}{2}n+\frac{A}{2}$.(3分)
设乙公司第n年市场占有率为bn,
根据图形可得:${b_n}=A+\frac{1}{2}A+\frac{1}{2^2}A+\frac{1}{2^3}A+…+\frac{1}{{{2^{n-1}}}}A$(5分)
=$({2-\frac{1}{{{2^{n-1}}}}})A$.
∴甲公司第n年市场占有率an=$\frac{A}{2}$n+$\frac{A}{2}$,乙公司第n年市场占有率bn=$({2-\frac{1}{{{2^{n-1}}}}})A$(6分)
(II)依题意,2012年为第20年,则${a_{20}}=\frac{A}{2}×20+\frac{A}{2}=\frac{21}{2}A>10A$,
${b_{20}}=(2-\frac{1}{{{2^{19}}}})A<2A$,(9分)
∴$\frac{{{b_{20}}}}{{{a_{20}}}}<\frac{2A}{10A}=20%$,即b20<20%•a20,(11分)
∴2012年会出现乙公司被甲公司兼并的局面.(12分)
点评 本题考查等差数列及等比数列模型,考查等差数列及等比数列前n项和公式,考查计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 当n=6时该命题不成立 | B. | 当n=6时该命题成立 | ||
| C. | 当n=8时该命题不成立 | D. | 当n=8时该命题成立 |
| A. | $-\sqrt{3}≤u≤\sqrt{3}$ | B. | $u≥\sqrt{3}$或$u≤-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}≤u≤\frac{{\sqrt{3}}}{3}$ | D. | $u≥\frac{{\sqrt{3}}}{3}$或$u≤-\frac{{\sqrt{3}}}{3}$ |
| A. | y与x成正线性相关关系 | |
| B. | 当商品销售价格提高1元时,商品的销售量减少200件 | |
| C. | 当销售价格为10元/件时,销售量为100件 | |
| D. | 当销售价格为10元/件时,销售量为100件左右 |
| A. | (-$\frac{3}{2}$,-$\frac{18}{5}$) | B. | ($\frac{4}{3}$,-$\frac{4}{3}$) | C. | (-2,-4) | D. | ($\frac{3}{2}$,-$\frac{6}{5}$) |
| A. | an=n | B. | an=n3-6n2+12n-6 | C. | an=$\frac{1}{2}$n2-$\frac{1}{2}$n+1 | D. | an=$\frac{6}{{n}^{2}-6n+11}$ |
 如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )