题目内容
17.用与球心距离为1的平面去截球所得的截面面积为π,则球的表面积为( )| A. | 2π | B. | 4π | C. | 8π | D. | $\frac{8}{3}π$ |
分析 先求出截面的半径r=1,再求出球半径R=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,由此能求出球的表面积.
解答 解:∵用与球心距离为1的平面去截球所得的截面面积为π,
∴截面的半径r=1,
∴球半径R=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴球的表面积S=4πR2=8π.
故选:C.
点评 本题考查球的表面积的求法,是基础题,解题时要认真审题,注意球的体积公式和表面积公式的合理运用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
8.函数y=sinx-2x的导数是( )
| A. | cosx-2x | B. | cosx-2x•ln2 | C. | -cosx+2x | D. | -cosx-2x•ln2 |
2.如图是某多面体的三视图,网格纸上小正方形的边长为1,则该多面体的体积为( )
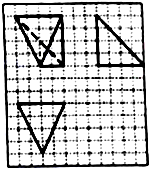

| A. | 32 | B. | $\frac{64}{3}$ | C. | 16 | D. | $\frac{32}{3}$ |
6.函数f(x)=$\frac{lg({x}^{2}-1)}{\sqrt{{x}^{2}-x-2}}$的定义域为( )
| A. | (-∞,-2)∪(1,+∞) | B. | (-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (1,2) |
7.函数y=sin2x图象上的某点P($\frac{π}{12}$,m)可以由函数y=cos(2x-$\frac{π}{4}$)上的某点Q向左平移n(n>0)个单位长度得到,则mn的最小值为( )
| A. | $\frac{5π}{24}$ | B. | $\frac{5π}{48}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{12}$ |
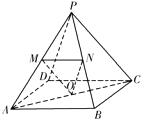 如图,在棱长均相等的正四棱锥P-ABCD最终,O为底面正方形的重心,M,N分别为侧棱PA,PB的中点,有下列结论:
如图,在棱长均相等的正四棱锥P-ABCD最终,O为底面正方形的重心,M,N分别为侧棱PA,PB的中点,有下列结论: