题目内容
2.已知函数f(x)=e2x-ax2+bx-1,其中a,b∈R,e为自然对数的底数,若f(1)=0,f′(x)是f(x)的导函数,函数f′(x)在区间(0,1)内有两个零点,则a的取值范围是( )| A. | (e2-3,e2+1) | B. | (e2-3,+∞) | C. | (-∞,2e2+2) | D. | (2e2-6,2e2+2) |
分析 利用f(1)=0得出a,b的关系,根据f′(x)=0有两解可知y=2e2x与y=2ax+a+1-e2的函数图象在(0,1)上有两个交点,做出两函数图象,根据图象判断a的范围.
解答 解:∵f(1)=0,∴e2-a+b-1=0,∴b=-e2+a+1,
∴f(x)=e2x-ax2+(-e2+a+1)x-1,
∴f′(x)=2e2x-2ax-e2+a+1,
令f′(x)=0得2e2x=2ax-a-1+e2,
∵函数f′(x)在区间(0,1)内有两个零点,
∴y=2e2x与y=2ax-a-1+e2的函数图象在(0,1)上有两个交点,
作出y=2e2x与y=2ax-a-1+e2=a(2x-1)+e2-1函数图象,如图所示:
若直线y=2ax-a-1+e2经过点(1,2e2),则a=e2+1,
若直线y=2ax-a-1+e2经过点(0,2),则a=e2-3,
∴e2-3<a<e2+1.
故选A.
点评 本题考查的知识点是函数零点与函数图象的关系,转化思想,分类说讨论思想,中档题.

练习册系列答案
相关题目
17.已知四棱锥P-ABCD中,侧棱都相等,底面是边长为$2\sqrt{2}$的正方形,底面中心为O,以PO为直径的球经过侧棱中点,则该球的体积为( )
| A. | $\frac{{8\sqrt{2}}}{3}π$ | B. | $\frac{{4\sqrt{2}}}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{32}{3}π$ |
7.函数y=sin2x图象上的某点P($\frac{π}{12}$,m)可以由函数y=cos(2x-$\frac{π}{4}$)上的某点Q向左平移n(n>0)个单位长度得到,则mn的最小值为( )
| A. | $\frac{5π}{24}$ | B. | $\frac{5π}{48}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{12}$ |
14.函数y=log2(3x2-7x+2)的单调减区间为( )
| A. | ($\frac{7}{6}$,+∞) | B. | (-∞,$\frac{7}{6}$) | C. | (-∞,$\frac{1}{3}$) | D. | (2,+∞) |
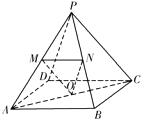 如图,在棱长均相等的正四棱锥P-ABCD最终,O为底面正方形的重心,M,N分别为侧棱PA,PB的中点,有下列结论:
如图,在棱长均相等的正四棱锥P-ABCD最终,O为底面正方形的重心,M,N分别为侧棱PA,PB的中点,有下列结论:
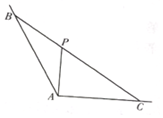 如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.
如图,∠BAC=$\frac{2π}{3}$,P为∠BAC内部一点,过点P的直线与∠BAC的两边交于点B,C,且PA⊥AC,AP=$\sqrt{3}$.