题目内容
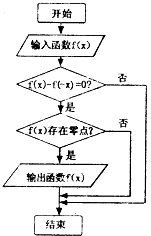
某程序框图如图所示,现输入四个函数,则可输出的函数是( )

| A、f(x)=ex |
| B、f(x)=x2+2 |
| C、f(x)=2x+2-x |
| D、f(x)=log2|x| |
考点:程序框图
专题:
分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件①f(x)-f(-x)=0,即函数f(x)为偶函数;②f(x)存在零点,即函数图象与x轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
解答:
解:由程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:
该程序的作用是输出满足条件①f(x)-f(-x)=0,即函数f(x)为偶函数,
②f(x)存在零点,即函数图象与x轴有交点.
∵A中f(x)=ex不是偶函数且无零点,故不满足条件①②;
∵B中f(x)=x2+2是偶函数但无零点,故不满足条件②;
∵C中,函数f(x)=2x+2-x是偶函数但无零点,故不满足条件②;
∵D中,函数f(x)=log2|x|是偶函数且有零点±1,故满足条件①②;
故可输出的函数是f(x)=log2|x|,
故选:D
该程序的作用是输出满足条件①f(x)-f(-x)=0,即函数f(x)为偶函数,
②f(x)存在零点,即函数图象与x轴有交点.
∵A中f(x)=ex不是偶函数且无零点,故不满足条件①②;
∵B中f(x)=x2+2是偶函数但无零点,故不满足条件②;
∵C中,函数f(x)=2x+2-x是偶函数但无零点,故不满足条件②;
∵D中,函数f(x)=log2|x|是偶函数且有零点±1,故满足条件①②;
故可输出的函数是f(x)=log2|x|,
故选:D
点评:本题考查的知识点是程序框图,其中根据程序框图分析出程序的功能是解答的关键.

练习册系列答案
相关题目
函数f(x)=x2-2lnx的增区间为( )
| A、(1,+∞) | ||
| B、(0,1) | ||
C、(
| ||
D、(0,
|
关于x的不等式x2-ax+a>0(a∈R)在R上恒成立的充分不必要条件是( )
| A、a<0或a>4 |
| B、0<a<2 |
| C、0<a<4 |
| D、0<a<8 |
已知曲线C1的参数方程
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系曲线,C2的极坐标方程为ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为(2,
).设P为C1上任意一点,则|PA|2+|PB|2+|PC|2+|PD|2的取值范围是( )
|
| π |
| 3 |
| A、[12,52] |
| B、[32,52] |
| C、[12,32] |
| D、[20,32] |
已知向量
,
满足|
|=1,|
|=2,
与
的夹角为60°,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
| C、1 | ||
| D、3 |
已知平面向量
=(0,1),
=(2,1),|λ
+
|=2,则λ=( )
| a |
| b |
| a |
| b |
A、1+
| ||
B、
| ||
| C、2 | ||
| D、-1 |

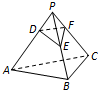 如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )
如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )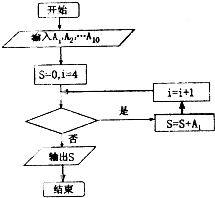 如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )
如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )