题目内容
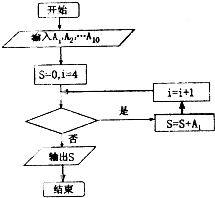 如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )
如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )| 分组 | [145,150) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) | [190,195) |
| 人数 | 146 | 251 | 352 | 510 | 618 | 522 | 388 | 293 | 108 | 89 |
| A、i<6? | B、i<7? |
| C、i<8? | D、i<9? |
考点:程序框图
专题:概率与统计,算法和程序框图
分析:该流程图的目的是算出身高在[160,180)内的学生人数,因此循环体需计算i=4、5、6、7时,四个Ai的和,由此可得判断框内应填写的条件是:“i<8”.
解答:
解:为了统计身高在[160,180)内的学生人数,先算出从160到180的小组分别有
[160,1165),[165,170),[170,175),[175,180)共有四组,分别为第4组、第5组、第6组和第7组.
因此,当i=4时开始,直到i=7时算出这四组的频数之和,
说明i≥8时结束循环而输出结果,可得判断框内应填写的条件是:“i<8”
故选:C
[160,1165),[165,170),[170,175),[175,180)共有四组,分别为第4组、第5组、第6组和第7组.
因此,当i=4时开始,直到i=7时算出这四组的频数之和,
说明i≥8时结束循环而输出结果,可得判断框内应填写的条件是:“i<8”
故选:C
点评:本题以统计条形图为载体,计算身高在[160,180)内的学生人数,考查了频率直方分布图的理解和循环结构的程序框图等知识,属于基础题.

练习册系列答案
相关题目
设f(x),g(x)分别是定义在R上的奇函数和偶函数,当f′(x)g(x)-f(x)g′(x)<0对任意x∈[0,+∞)恒成立,则不等式
<0的解集是( )
| f(x) |
| g(x) |
| A、(-∞,0] |
| B、[0,+∞) |
| C、(-∞,0) |
| D、(0,+∞) |
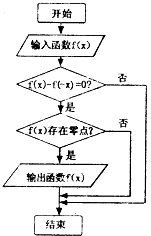
某程序框图如图所示,现输入四个函数,则可输出的函数是( )

| A、f(x)=ex |
| B、f(x)=x2+2 |
| C、f(x)=2x+2-x |
| D、f(x)=log2|x| |
设[x]表示不大于x的最大整数,则函数f(x)=lg2x-[lgx]-2的零点个数是( )
| A、4 | B、3 | C、2 | D、1 |
将自然数的前5个数:(1)排成1,2,3,4,5;(2)排成5,4,3,2,1;(3)排成2,1,5,3,4;(4)排成4,1,5,3,2.那么,可以叫做数列的只有( )
| A、(1) |
| B、(1),(2) |
| C、(1),(2),(3) |
| D、(1),(2),(3),(4) |
某学校数学教师中有高级教师6人,一级教师12人,二级教师18人,从中抽取一个容量为n的样本,如果采取系统抽样和分层抽样的方法抽取,不用剔除个体;如果样本容量增加1个,那么在采用系统抽样时需要在总体中先剔除1个个体.则n值为( )
| A、3 | B、6 | C、12 | D、18 |
停车站划出一排10个停车位置,今有6辆不同的车需要停放,若要求剩余的4个空车位连在一起,则不同的停车方法有( )
A、
| ||||
B、2
| ||||
C、6
| ||||
D、7
|
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图所示,则φ=( )

| π |
| 2 |

A、-
| ||
B、
| ||
C、-
| ||
D、
|