题目内容
已知平面向量
=（0，1），
=（2，1），|λ
+
|=2，则λ=（ ）
| a |
| b |
| a |
| b |
A、1+
| ||
B、
| ||
| C、2 | ||
| D、-1 |
考点：向量的模
专题：平面向量及应用
分析：利用向量数量积的性质和模的计算公式即可得出．
解答：
解：∵平面向量
=（0，1）
=（2，1），
∴|
|=1，|
|=
=
，
•
=1．
∴|λ
+
|=
=
=2，
∴λ2×12+5+2λ=4，
化为λ2+2λ+1=0，解得λ=-1．
故选：D
| a |
| b |
∴|
| a |
| b |
| 22+12 |
| 5 |
| a |
| b |
∴|λ
| a |
| b |
(λ
|
λ2
|
∴λ2×12+5+2λ=4，
化为λ2+2λ+1=0，解得λ=-1．
故选：D
点评：本题考查了向量数量积的性质和模的计算公式，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
某程序框图如图所示，现输入四个函数，则可输出的函数是（ ）
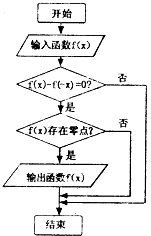
| A、f（x）=ex |
| B、f（x）=x2+2 |
| C、f（x）=2x+2-x |
| D、f（x）=log2|x| |
停车站划出一排10个停车位置，今有6辆不同的车需要停放，若要求剩余的4个空车位连在一起，则不同的停车方法有（ ）
A、
| ||||
B、2
| ||||
C、6
| ||||
D、7
|
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜
）的部分图象如图所示，则φ=（ ）
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
如图，直线a在α内，b在β内，α⊥β，α∩β=c，∠1=∠2=60°则a、b所成角θ的余弦值为（ ）
| A、1 | ||
B、-
| ||
C、
| ||
D、
|
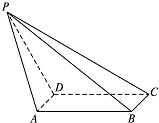如图，在四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PC=2