题目内容
6.已知F1、F2是椭圆C1与双曲线C2的公共焦点,点P是C1与C2的公共点,若椭圆C1的离心率e1∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$],∠F1PF2=$\frac{π}{2}$,则双曲线C2的离心率e2的最小值为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 设椭圆及双曲线方程,利用定义求得丨PF1丨=a1+a2,丨PF2丨=a1-a2,利用勾股定理及椭圆、双曲线的离心率公式,求得$\frac{1}{{{e}_{1}}^{2}}$+$\frac{1}{{{e}_{2}}^{2}}$=2,利用椭圆的离心率范围,即可求得e2的最小值.
解答 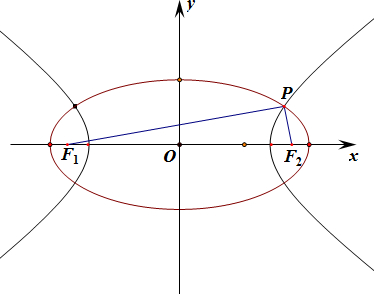 解:设椭圆的标准方程:$\frac{{x}^{2}}{{{a}_{1}}^{2}}$+$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1(a1>b1>0),
解:设椭圆的标准方程:$\frac{{x}^{2}}{{{a}_{1}}^{2}}$+$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1(a1>b1>0),
双曲线的标准方程:$\frac{{x}^{2}}{{{a}_{2}}^{2}}$-$\frac{{y}^{2}}{{{b}_{2}}^{2}}$=1(a2>0,b2>0),
设P位于第一象限,半焦距为c,
由椭圆和双曲线的定义可知丨PF1丨+丨PF2丨=2a1,
丨PF1丨-丨PF2丨=2a2,
解得丨PF1丨=a1+a2,丨PF2丨=a1-a2,
由∠F1PF2=$\frac{π}{2}$,则丨PF1丨2+丨PF2丨2=丨F1F2丨2,
∴(a1+a2)2+(a1-a2)2=(2c)2,即a12+a22=2c2,
即有$\frac{{{a}_{1}}^{2}}{{c}^{2}}$+$\frac{{{a}_{2}}^{2}}{{c}^{2}}$=2,
即为$\frac{1}{{{e}_{1}}^{2}}$+$\frac{1}{{{e}_{2}}^{2}}$=2,
由e1∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$],
可得$\frac{1}{{{e}_{1}}^{2}}$∈[$\frac{4}{3}$,2),
则$\frac{1}{{{e}_{2}}^{2}}$∈(0,$\frac{2}{3}$].
则e2≥$\frac{\sqrt{6}}{2}$,
即有双曲线C2的离心率e2的最小值为$\frac{\sqrt{6}}{2}$.
故选:B.
点评 本题考查椭圆及双曲线的定义及简单几何性质,考查数形结合思想,考查运算求解能力,属于中档题.

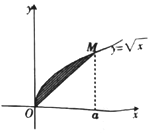 如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )
如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
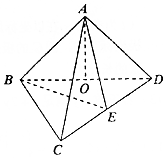 如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.
如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.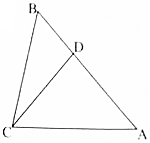
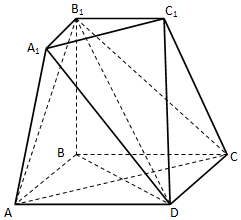 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)