题目内容
6.从0,1,2,3,4,5,6中每次取出5个来排列,可以组成多少个1不在百位、2不在个位且没有重复数字的五位数?分析 由题意分两类,第一类:1在个位的;第二类:1不在个位也不在百位,根据分类加法原理可得.
解答 解:由1不在百位,可分为以下两类
第一类:1在个位的共有A43=24个;
第二类:1不在个位也不在百位的共有A31A31A32=54个.
所以1不在百位且2不在个位的共有24+54=78个.
点评 本题主要考查了分类计数原理,关键是分类,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.f(x)=$\sqrt{x}$lnx在点(4,f(4))处的切线方程为( )
| A. | (ln2+1)x-2y+4ln2-4=0 | B. | (ln4+1)x-2y+7ln4-1=0 | ||
| C. | (ln4+1)x-2y+8ln2-4=0 | D. | (ln2+1)x+2y+7ln2-4=0 |
9. 阅读右边的程序框图,运行相应的程序,输出k的值是( )
阅读右边的程序框图,运行相应的程序,输出k的值是( )
 阅读右边的程序框图,运行相应的程序,输出k的值是( )
阅读右边的程序框图,运行相应的程序,输出k的值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
6.已知F1、F2是椭圆C1与双曲线C2的公共焦点,点P是C1与C2的公共点,若椭圆C1的离心率e1∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$],∠F1PF2=$\frac{π}{2}$,则双曲线C2的离心率e2的最小值为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
11.在正项等比数列{an}和正项等差数列{bn}中,已知a1,a2017的等比中项与b1,b2017的等差中项相等,且$\frac{1}{{b}_{1}}$+$\frac{4}{{b}_{2017}}$≤1,当a1009取得最小值时,等差数列{bn}的公差d的取值集合为( )
| A. | {d|d≥$\frac{1}{672}$} | B. | {d|0<d<$\frac{1}{672}$} | C. | {$\frac{1}{672}$} | D. | {d|d≥$\frac{3}{2017}$} |
16.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$,若z=2x+y的最小值为1,则a=( )
| A. | 1 | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
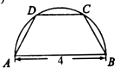 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.