Question

14．平面内三点A，B，C满足|$\overrightarrow{BA}$|=3，|$\overrightarrow{BC}$|=4，$\overrightarrow{BA}$$•\overrightarrow{BC}$=0，M，N为平面内的动点，且$\overrightarrow{AM}$为单位向量，若$\overrightarrow{MC}$=2$\overrightarrow{MN}$，则|$\overrightarrow{BN}$|的最大值与最小值的和为（　　）

• A． 10
• B． 8
• C． 7
• D． 5

Answer 1

分析 建立坐标系，设M（cosθ，3+sinθ），求出|$\overrightarrow{BN}$|关于θ的函数，根据三角函数的性质求出|$\overrightarrow{BN}$|的最值．

解答 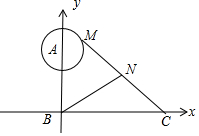解：∵$\overrightarrow{BA}$$•\overrightarrow{BC}$=0，∴BA⊥BC，
∵|$\overrightarrow{AM}$|=1，∴M在以A为原点，1为半径的圆A上，
∵$\overrightarrow{MC}$=2$\overrightarrow{MN}$，∴N是MC的中点，
以BC，BA为坐标轴建立坐标系，如图：则B（0，0），C（4，0），A（0，3），
设M（cosθ，3+sinθ），则N（$\frac{1}{2}$cosθ+2，$\frac{1}{2}$sinθ+$\frac{3}{2}$），
∴|$\overrightarrow{BN}$|=$\sqrt{（\frac{1}{2}cosθ+2）^{2}+（\frac{1}{2}sinθ+\frac{3}{2}）^{2}}$=$\sqrt{\frac{13}{2}+2cosθ+\frac{3}{2}sinθ}$=$\sqrt{\frac{13}{2}+\frac{5}{2}sin（θ+γ）}$，
∴|$\overrightarrow{BN}$|的最大值为$\sqrt{\frac{13}{2}+\frac{5}{2}}$=3，最小值为$\sqrt{\frac{13}{2}-\frac{5}{2}}$=2，
∴|$\overrightarrow{BN}$|的最大值与最小值的和为5．
故选D．

点评 本题考查了平面向量的运算，属于中档题．