已知函数f(x)=$\left\{\begin{array}{l}1-|x+1|.x＜1\\{x^2}-4x+2.x≥1\end{array}$.则函数g(x)=2|x|f个．A．1B．2C．3D．4 题目和参考答案——青夏教育精英家教网——

题目内容

11．已知函数f（x）=$\left\{\begin{array}{l}1-|x+1|，x＜1\\{x^2}-4x+2，x≥1\end{array}$，则函数g（x）=2^|x|f（x）-2的零点个数为（　　）个．

A．

1

B．

2

C．

3

D．

4

分析由2^|x|f（x）-2=0，可得f（x）=2^1-|x|，问题转化为函数f（x）=$\left\{\begin{array}{l}1-|x+1|，x＜1\\{x^2}-4x+2，x≥1\end{array}$，与h（x）=2^1-|x|的交点个数．作出函数的图象，可得结论．

解答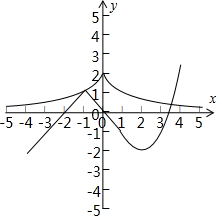解：由2^|x|f（x）-2=0，可得f（x）=2^1-|x|，
问题转化为函数f（x）=$\left\{\begin{array}{l}1-|x+1|，x＜1\\{x^2}-4x+2，x≥1\end{array}$，与h（x）=2^1-|x|的交点个数．
在同一坐标系中，作出两个函数的图象，
可得交点有2个，所以函数g（x）=2^|x|f（x）-2的零点个数为2个，
故选：B．

点评本题考查函数零点的判断，考查数形结合的数学思想，正确转化，作出函数的图象是关键．

练习册系列答案

龙江中考系列答案

状元陪练系列答案

2016中考168系列答案

创新设计导学课堂系列答案

创新设计学业水平考试系列答案

金状元直击期末系列答案

小学生智能优化卷系列答案

师大测评卷提炼知识点系列答案

挑战100分期末天天练系列答案

单元达标名校调研系列答案

相关题目

1．设数列{a_n}的通项公式a_n=2n-1，数列{b_n}满足a₁b₁+a₂b₂+a₃b₃+…+a_nb_n=$\frac{20}{9}$+（$\frac{2n}{3}$-$\frac{5}{9}$）×2${\;}^{2n+{2}^{\;}}$，则数列{b_n}的通项公式b_n=4ⁿ．

2．在锐角△ABC中，内角A，B，C的对边分别是a，b，c，已知$\frac{\sqrt{3}}{3}$sin2C+cos（A+B）=0．
（Ⅰ）求C；
（Ⅱ）若a=4$\sqrt{3}$sinA，求△ABC面积的最大值．

19．已知函数f（x）=4tan（x+$\frac{π}{6}$）cos²（x+$\frac{π}{6}$）-1．
（Ⅰ）求f（x）的定义域与最小正周期；
（Ⅱ）讨论f（x）在区间（0，$\frac{π}{3}$）上的单调性．

6．已知F₁、F₂是椭圆C₁与双曲线C₂的公共焦点，点P是C₁与C₂的公共点，若椭圆C₁的离心率e₁∈（$\frac{\sqrt{2}}{2}$，$\frac{\sqrt{3}}{2}$]，∠F₁PF₂=$\frac{π}{2}$，则双曲线C₂的离心率e₂的最小值为（　　）

$\frac{\sqrt{5}}{2}$

$\frac{\sqrt{6}}{2}$

4．求函数f（x）=x²+x在区间[x₀，x₀+△x]上的平均变化率，并求当x₀=1，△x=0.1时的平均变化率．

11．在正项等比数列{a_n}和正项等差数列{b_n}中，已知a₁，a₂₀₁₇的等比中项与b₁，b₂₀₁₇的等差中项相等，且$\frac{1}{{b}_{1}}$+$\frac{4}{{b}_{2017}}$≤1，当a₁₀₀₉取得最小值时，等差数列{b_n}的公差d的取值集合为（　　）

{d|d≥$\frac{1}{672}$}

{d|0＜d＜$\frac{1}{672}$}

{$\frac{1}{672}$}

{d|d≥$\frac{3}{2017}$}

8．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{x}，x＞0}\\{-{x}^{2}-4x，x≤0}\end{array}\right.$则此函数图象上关于原点对称的点有（　　）

9．中心在原点的椭圆C₁与双曲线C₂具有相同的焦点，F₁（-c，0），F₂（c，0），P为C₁与C₂在第一象限的交点，|PF₁|=|F₁F₂|且|PF₂|=5，若椭圆C₁的离心率${e_1}∈（{\frac{3}{5}，\frac{2}{3}}）$，则双曲线的离心率e₂的范围是（　　）

$（{\frac{3}{2}，\frac{5}{3}}）$

$（{\frac{5}{3}，2}）$

$（{\frac{3}{2}，3}）$