题目内容
3.如图,在△ABC中,B=$\frac{π}{4}$,点D在边AB上,BD=2,且DA=DC,AC=2$\sqrt{2}$,则∠DCA=$\frac{π}{12}$或$\frac{5π}{12}$或$\frac{π}{4}$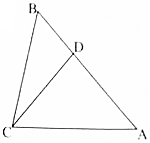
分析 设∠DCA=θ,DC=x,根据余弦定理和正弦定理可得cos2θ(2sin2θ-1)=0,再解得即可
解答 解:设∠DCA=θ,DC=x,
在△BDC中,由余弦定理可得AC2=x2+x2-2x2cos(2π-2θ),
即4=x2(1+cos2θ),
∴x2=$\frac{4}{1+cos2θ}$
在△BCD中,∠DCB=π-B-∠BDC=$\frac{3π}{4}$-2θ,
由正弦定理可得$\frac{BD}{sin∠BDC}$=$\frac{CD}{sinB}$,
即x=$\frac{2×\frac{\sqrt{2}}{2}}{sin(\frac{3π}{4}-2θ)}$=$\frac{2}{cos2θ+sin2θ}$,
∴x2=$\frac{4}{1+2sin2θcos2θ}$,
∴$\frac{4}{1+cos2θ}$=$\frac{4}{1+2sin2θcos2θ}$,
∴1+cos2θ=1+2sin2θcos2θ,
∴cos2θ(2sin2θ-1)=0,
∴cos2θ=0或2sin2θ-1=0,
解得2θ=$\frac{π}{2}$或2θ=$\frac{π}{6}$或2θ=$\frac{5π}{6}$
∴θ=$\frac{π}{4}$或θ=$\frac{π}{12}$或θ=$\frac{5π}{12}$,
故答案为:$\frac{π}{12}$或$\frac{π}{4}$或$\frac{5π}{12}$
点评 本题考查了正弦定理和余弦定理以及三角函数的化简,考查了学生的运算能力,属于中档题

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
6.已知F1、F2是椭圆C1与双曲线C2的公共焦点,点P是C1与C2的公共点,若椭圆C1的离心率e1∈($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$],∠F1PF2=$\frac{π}{2}$,则双曲线C2的离心率e2的最小值为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
11.在正项等比数列{an}和正项等差数列{bn}中,已知a1,a2017的等比中项与b1,b2017的等差中项相等,且$\frac{1}{{b}_{1}}$+$\frac{4}{{b}_{2017}}$≤1,当a1009取得最小值时,等差数列{bn}的公差d的取值集合为( )
| A. | {d|d≥$\frac{1}{672}$} | B. | {d|0<d<$\frac{1}{672}$} | C. | {$\frac{1}{672}$} | D. | {d|d≥$\frac{3}{2017}$} |
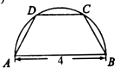 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.