题目内容
20.某高中学校为了解学生体质情况,从高一和高二两个年级分别随机抽取了40名男同学进行“引体向上”项目测试.样本的测试成绩均在0至30个之间,按照[0,5),[5,10),[10,15),[15,20),[20,25),[25,30]的分组分别作出频率分布直方图.记样本中高一年级的“引体向上”成绩的方差为s12,高二年级的“引体向上”成绩的方差为s22.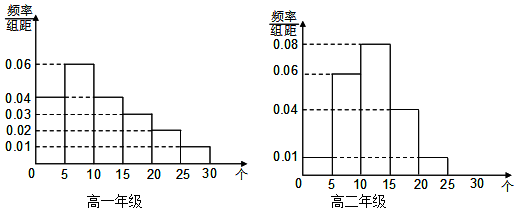
(Ⅰ)已知该学校高二年级男同学有500人,估计该学校高二年级男同学引体向上成绩不少于10个的人数;
(Ⅱ)从样本中高一年级的成绩不小于20个男同学中随机抽取2人,求至少有1人成绩在[25,30]中的概率.
(Ⅲ)比较s12与s22的大小(只需写出结果).
分析 (Ⅰ)先求出样本中高二年级男同学引体向上成绩不少于10个的频率,由此能估计该学校高二年级男同学引体向上成绩不少于10个的人数.
(Ⅱ)记“从样本中高一年级的成绩不小于20个的同学中随机抽取2人,至少有1人成绩在[25,30]中”为事件M,样本中高一年级的成绩在[20,25)的人数为4人,记这4名同学为A1,A2,A2,A4,样本中高一年级的成绩在[25,30]的人数为2人,记这两名同学为B1,B2,由此利用列举法能求出至少有1人成绩在[25,30]中的概率.
(Ⅲ)由频率分布直方图能比较${{S}_{1}}^{2}$,${{S}_{2}}^{2}$的大小.
解答 解:(Ⅰ)因为样本中高二年级男同学引体向上成绩不少于10个的频率为(0.08+0.04+0.01)×5=0.65,(2分)
所以估计该学校高二年级男同学引体向上成绩不少于10个的人数为:
500×0.65=325人.(4分)
(Ⅱ)记“从样本中高一年级的成绩不小于20个的同学中随机抽取2人,
至少有1人成绩在[25,30]中”为事件M,(5分)
样本中高一年级的成绩在[20,25)的人数为40×0.02×5=4人,
记这4名同学为A1,A2,A2,A4,
样本中高一年级的成绩在[25,30]的人数为40×0.01×5=2人,
记这两名同学为B1,B2,(6分)
则从样本中高一年级的成绩不小于20个的同学中,随机抽取2人,所有可能的结果有15种,分别为:
(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),
(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2),(8分)
事件M包含的结果有9种,分别是:
(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),
(A3,B2),(A4,B1),(A4,B2),(B1,B2),
所以至少有1人成绩在[25,30]中的概率P(M)=$\frac{9}{15}=\frac{3}{5}$.(11分)
(Ⅲ)${{S}_{1}}^{2}$>${{S}_{2}}^{2}$.(13分)
点评 本题考查频率分布直方图的应用,考查概率的求法,涉及到频率分布直方图的性质、列举法,方差等基础知识,考查数据处理能力、运算求解能力,考查数形结合思想、集合思想,是基础题.

 名校课堂系列答案
名校课堂系列答案| A. | (0,$\frac{1}{e}$) | B. | [$\frac{1}{4}$,$\frac{1}{e}$) | C. | (0,$\frac{1}{4}$] | D. | ($\frac{1}{4}$,e) |
| A. | 1 | B. | -1 | C. | ±1 | D. | 2 |
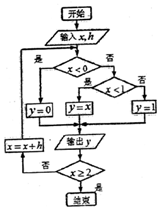 如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )
如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )| A. | 1 | B. | 1.5 | C. | 2.5 | D. | 3 |
| A. | i | B. | -i | C. | 1 | D. | -1 |