题目内容

设数列{an}，{an2} （n∈N*）都是等差数列，若a1=2，则a22+a33+a44+a55等于（　　）
A、60B、62C、63D、66
考点：等差数列的性质
专题：等差数列与等比数列
分析：设数列{an}的公差为d，则由题意可得2a22 =a12+a32，即2（2+d）2=22+（2+2d）2，解得d的值，可得an的通项公式，从而求得a22+a33+a44+a55 的值．
解答： 解：∵数列{an}，{an2} （n∈N*）都是等差数列，a1=2，设数列{an}的公差为d，
则有2a22 =a12+a32，即 2（2+d）2=22+（2+2d）2，
解得d=0，
∴an=2，
∴an2=4，
∴a22+a33+a44+a55=4+8+16+32=60，
故选：A．
点评：本题主要考查等差数列的定义和性质，等差数列的通项公式，属于中档题．
练习册系列答案
相关题目
已知函数f(x)=
1
3
x3+x2+ax．
（1）若f（x）在区间[1，+∞）单调递增，求a的最小值；
（2）若g(x)=
1
ex
，对?x1∈[
1
2
，2]，?x2∈[
1
2
，2]，使f′（x1）≤g（x2）成立，求a的范围．
设函数f（x）=ax2+x．已知f（3）＜f（4），且当n≥8，n∈N*时，f（n）＞f（n+1）恒成立，则实数a的取值范围是
 
．
在（x+3）（x-1）6的展开式中，x4的系数是
 
（用数字作答）．
正三棱柱的左视图如图所示，则该正三棱柱的侧面积为（　　）
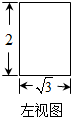
A、4
B、12
C、
4
3
3
D、24
若函数f（x）同时具有以下两个性质：①f（x）是偶函数，②对任意实数x，都有f（
π
4
+x）=f（
π
4
-x），则f（x）的解析式可以是（　　）
A、f（x）=cosx
B、f（x）=cos（2x+
π
2
）
C、f（x）=sin（4x+
π
2
）
D、f（x）=cos6x
一个算法的程序框图如图所示，如果输入的x的值为2014，则输出的i的结果为（　　）
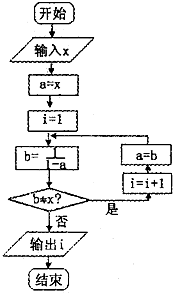
A、3B、5C、6D、8
已知椭圆C经过点A（0，2），B（
1
2
，
3
）．
（Ⅰ）求椭圆C的方程．
（Ⅱ）设P（x0，y0）为椭圆C上的动点，求x20+2y0的最大值．
在平面直角坐标系中，已知
a
=(2mx，y-1)，
b
=(2x，y+1)，其中m∈R，
a
⊥
b
，动点M（x，y）的轨迹为C．
（1）求轨迹C的方程，并说明该轨迹方程所表示曲线的形状；
（2）当m=
1
8
时，设过定点P（0，2）的直线l与轨迹C交于不同的两点A、B，且∠AOB为锐角（其中O为坐标原点），求直线l的斜率k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网