题目内容
当x∈(1,+∞)时,用数学归纳法证明:?n∈N*,ex-1>
.(n!=1•2•3•…•(n-1)n)
| xn |
| n! |
考点:数学归纳法
专题:导数的概念及应用,点列、递归数列与数学归纳法
分析:构造函数gn(x)=ex-1-
,当n=1时,只需证明g1(x)=ex-1-x>0(利用导数法易证);当x∈(1,+∞)时,假设n=k时不等式成立,即gk(x)=ex-1-
>0,去证明
当n=k+1时,不等式也成立,从而证得结论成立即可.
| xn |
| n! |
| xk |
| k! |
当n=k+1时,不等式也成立,从而证得结论成立即可.
解答:
证明:设gn(x)=ex-1-
,
当n=1时,只需证明g1(x)=ex-1-x>0,当x∈(1,+∞)时,g1′(x)=ex-1-1>0,
所以g1(x)=ex-1-x在(1,+∞)上是增函数,∴g1(x)>g1(1)=e0-1=0,即ex-1>x;
当x∈(1,+∞)时,
假设n=k时不等式成立,即gk(x)=ex-1-
>0,
当n=k+1时,
因为gk+1′(x)=ex-1-
=ex-1-
>0,
所以gk+1(x)在(1,+∞)上也是增函数.
所以g(x)>gk+1(1)=e0-
=1-
>0,
即当n=k+1时,不等式成立.
由归纳原理,知当x∈(1,+∞)时,?n∈N*,ex-1-
.
| xn |
| n! |
当n=1时,只需证明g1(x)=ex-1-x>0,当x∈(1,+∞)时,g1′(x)=ex-1-1>0,
所以g1(x)=ex-1-x在(1,+∞)上是增函数,∴g1(x)>g1(1)=e0-1=0,即ex-1>x;
当x∈(1,+∞)时,
假设n=k时不等式成立,即gk(x)=ex-1-
| xk |
| k! |
当n=k+1时,
因为gk+1′(x)=ex-1-
| (k+1)xk |
| (k+1)! |
| xk |
| k! |
所以gk+1(x)在(1,+∞)上也是增函数.
所以g(x)>gk+1(1)=e0-
| 1 |
| (k+1)! |
| 1 |
| (k+1)! |
即当n=k+1时,不等式成立.
由归纳原理,知当x∈(1,+∞)时,?n∈N*,ex-1-
| xn |
| n! |
点评:本题考查数学归纳法的应用,考查构造函数思想与导数法判断函数的单调性质的综合应用,考察推理证明能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=alog2x+blog3x+2且f(
)=4,则f(2015)的值为( )
| 1 |
| 2015 |
| A、-4 | B、2 | C、0 | D、-2 |
已知复数z=a+bi(a∈R,b∈R)且a+b=1,则下列结论错误的是( )
| A、z可能为实数 | ||||
| B、z不可能为纯虚数 | ||||
C、若z的共轭复数为z,则z•
| ||||
D、|z|的最小值为
|
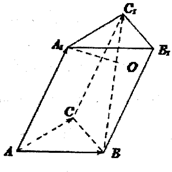 如图所示,三棱柱ABC-A1B1C1中,AA1=2AB=2AC=2.∠A1AB=∠A1AC=∠BAC=60°,设
如图所示,三棱柱ABC-A1B1C1中,AA1=2AB=2AC=2.∠A1AB=∠A1AC=∠BAC=60°,设