Question

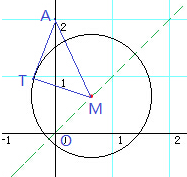
已知点 A（0，2）为圆M：x²+y²-2ax-2ay=0外一点，圆M上存在点T使得∠MAT=45°，则实数a的取值范围是

 

．

Answer 1

考点：圆的一般方程

专题：直线与圆

分析：化标准方程易得圆的圆心为M（a，a），半径r=

2

a，由题意可得1≥

TM

AM

≥sin∠MAT，由距离公式可得a的不等式，解不等式可得．

解答： 解：化圆的方程为标准方程可得（x-a）²+（y-a）²=2a²，
∴圆的圆心为M（a，a），半径r=

2

|a|，
∴AM=

a2+(a-2)2

，TM=

2

|a|，
∵AM和TM长度固定，
∴当T为切点时，∠MAT最大，
∵圆M上存在点T使得∠MAT=45°，
∴若最大角度大于45°，则圆M上存在点T使得∠MAT=45°，
∴

TM

AM

=

2 |a|

a2+(a-2)2

≥sin∠MAT=sin45°=

2

2

，
整理可得a²+2a-2≥0，解得a≥

3

-1或a≤-

3

-1，
又

TM

AM

=

2 |a|

a2+(a-2)2

≤1，解得a≤1，
又点 A（0，2）为圆M：x²+y²-2ax-2ay=0外一点，
∴0²+2²-4a＞0，解得a＜1
综上可得

3

-1≤a＜1或a≤-

3

-1
故答案为：

3

-1≤a＜1或a≤-

3

-1

点评：本题考查圆的一般式方程和圆的性质，涉及距离公式的应用，属中档题．