Question

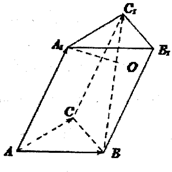如图所示，三棱柱ABC-A₁B₁C₁中，AA₁=2AB=2AC=2．∠A₁AB=∠A₁AC=∠BAC=60°，设

AB

=

a

，

AC

=

b

，

AA

=

c

．
（1）试用向量

a

，

b

，

c

表示

BC1

，并求|

BC1

|；
（2）在平行四边形BB₁C₁C内是否存在一点O，使得A₁O⊥平面BB₁C₁C，若不存在，请说明理由；若存在，试确定O点的位置．

Answer 1

考点：直线与平面垂直的判定,平面向量的基本定理及其意义

专题：空间位置关系与距离

分析：（1）利用向量的三角形法则可解；
（2）假设在平行四边形BB₁C₁C内存在一点O，使得A₁O⊥平面BB₁C₁C，

解答： 解：（1）因为几何体是三棱柱，
所以

BC1

=

BA

+

AC

+

CC1

=-

a

+

b

+

c

，
所以|

BC1

|²=

a

2+

b

2+

c

2-2

a

•

b

+2

b

•

c

-2

a

•

c

=1+1+4-2×1×1×cos60°+2×1×2×cos60°-2×1×2×cos60°=5，
所以|

BC1

|=

5

；
（2）假设在平行四边形BB₁C₁C内存在一点O，使得A₁O⊥平面BB₁C₁C；
过A₁作A₁D⊥平面ABC，因为∠A₁AB=∠A₁AC=∠BAC=60°，所以D在∠BAC的平分线AE上，A₁D⊥BC，又BC⊥AE，所以BC⊥平面AA₁E₁E，
过A₁作A₁O⊥EE₁，则A₁O⊥平面BB₁C₁C；
所以在平行四边形BB₁C₁C内存在一点O，使得A₁O⊥平面BB₁C₁C；假设正确．

点评：本题考查了向量的三角形法则以及线面垂直、面面垂直的判定定理和性质定理的运用，属于中档题．