题目内容
不等式
<0的解集为( )
| x-2 |
| |x|-1 |
| A、{x|1<x<2} |
| B、{x|x<2且x≠1} |
| C、{x|-1<x<2且x≠1} |
| D、{x|x<-1或1<x<2} |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:先去掉绝对值,再把分式不等式化为等价的一元二次不等式,从而求出解集来.
解答:
解:∵不等式
<0,
∴当x≥0时,原不等式可化为
<0,
等价于(x-2)(x-1)<0,
解得1<x<2;
当x<0时,原不等式可化为
<0,
即
>0,
等价于(x-2)(x+1)>0,
解得x>2,或x<-1;
∴x<-1;
综上,原不等式的解集为{x|x<-1,或1<x<2}.
故选:D.
| x-2 |
| |x|-1 |
∴当x≥0时,原不等式可化为
| x-2 |
| x-1 |
等价于(x-2)(x-1)<0,
解得1<x<2;
当x<0时,原不等式可化为
| x-2 |
| -x-1 |
即
| x-2 |
| x+1 |
等价于(x-2)(x+1)>0,
解得x>2,或x<-1;
∴x<-1;
综上,原不等式的解集为{x|x<-1,或1<x<2}.
故选:D.
点评:本题考查了含有绝对值的不等式的解法与应用问题,解题时应先去掉绝对值,再解不等式,是基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
在△ABC中,若AB=2,AC2+BC2=8,则△ABC面积的最大值为( )
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
把正整数按如图所示的规律排列,则从2003到2005的箭头方向依次为( )


| A、↓ 2004→ |
| B、↑ →2004 |
| C、2004→ ↑ |
| D、→2004 ↓ |
数列{an}的前n项和Sn=n2-9n,若5<ak<8,则k=( )
| A、6 | B、7 | C、8 | D、9 |
在复平面内,复数z=sin3+icos3对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
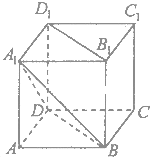 如图,在正方体ABCD-A1B1C1D1中,AB=2.
如图,在正方体ABCD-A1B1C1D1中,AB=2.