题目内容
已知函数f(x)=
+
的定义域为集合M,函数g(x)=|3-x|-|x-1|的值域为N.
(1)求M,N;
(2)求M∪N,M∩∁RN.
| 3-x |
| x-1 |
(1)求M,N;
(2)求M∪N,M∩∁RN.
考点:交、并、补集的混合运算
专题:集合
分析:(1)根据函数的定义域和值域即可求M,N;
(2)根据集合的基本运算即可求M∪N,M∩∁RN.
(2)根据集合的基本运算即可求M∪N,M∩∁RN.
解答:
解:(1)依题意,
,解得
,解得1≤x≤3,即M=[1,3].
g(x)=|3-x|-|x-1|=
,
当x<1时,g(x)∈{2};
当1≤x≤3时,g(x)=4-2x∈[-2,2];
当x>3时,g(x)∈{-2}
所以N=[-2,2]
(2)由(1)知M∪N=[-2,3].
CRN=(-∞,-2)∪(2,+∞),
所以M∩CRN=(2,3].
|
|
g(x)=|3-x|-|x-1|=
|
当x<1时,g(x)∈{2};
当1≤x≤3时,g(x)=4-2x∈[-2,2];
当x>3时,g(x)∈{-2}
所以N=[-2,2]
(2)由(1)知M∪N=[-2,3].
CRN=(-∞,-2)∪(2,+∞),
所以M∩CRN=(2,3].
点评:本题主要考查集合的基本运算,根据条件求出函数的定义域和值域是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f′(x)≥0,则a=f(
),b=f(
),c=f(
)的大小关系是( )
| 16 |
| 3 |
| 17 |
| 3 |
| 23 |
| 3 |
| A、c<b<a |
| B、c<a<b |
| C、a<c<b |
| D、a<b<c |
命题P:?x∈R,ax2+ax+1≥0为真命题,则实数a的取值范围是( )
| A、(0,4] |
| B、(-∞,4)∪(4,+∞) |
| C、(-∞,0]∪[4,+∞) |
| D、[0,4] |
函数y=
(a<0且a为常数)在区间(-∞,1]上有意义,则实数a的取值范围( )
| ax+1 |
| A、[-1,0) |
| B、(-1,0) |
| C、[-1,0] |
| D、(-1,+∞) |
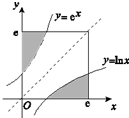 如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为
如图,由x=0,x=e,y=0,y=e,y=lnx,y=ex六条曲线共同围成的面积为