题目内容
已知对于任意x∈[0，2]
（1）若x2+2x+a＞0恒成立，求实数a的取值范围；
（2）若x2+2x+a＜2恒成立，求实数a的取值范围．
（1）若x2+2x+a＞0恒成立，求实数a的取值范围；
（2）若x2+2x+a＜2恒成立，求实数a的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：（1）转化x2+2x+a＞0恒成立，求出a的表达式，然后求表达式的最大值，即可得到实数a的取值范围；
（2）若x2+2x+a＜2恒成立，求出a的表达式，然后求表达式的最小值，即可得到实数a的取值范围．
（2）若x2+2x+a＜2恒成立，求出a的表达式，然后求表达式的最小值，即可得到实数a的取值范围．
解答：
解：（1）不等式x2+2x+a＞0恒成立，即a＞-x2-2x，在x∈[0，2]恒成立．
∵-x2-2x∈[-8，0]，
∴实数a的取值范围：（0，+∞）．
（2）x2+2x+a＜2恒成立，即a＜2-x2-2x，在x∈[0，2]恒成立．
∵2-x2-2x∈[-6，2]，
∴实数a的取值范围：（-∞，-6）．
∵-x2-2x∈[-8，0]，
∴实数a的取值范围：（0，+∞）．
（2）x2+2x+a＜2恒成立，即a＜2-x2-2x，在x∈[0，2]恒成立．
∵2-x2-2x∈[-6，2]，
∴实数a的取值范围：（-∞，-6）．
点评：本题考查二次函数最值的应用，函数的恒成立的应用，考查计算能力．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
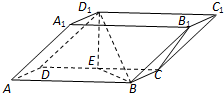如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD和侧面BCC1B1都是矩形，E是CD的中点，D1E⊥CD，AB=2BC=2．
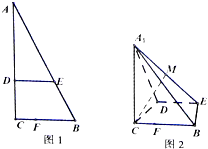如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E，F分别是AC，AB CB上的点，且DE∥BC，DE=2，CF=1，将△ADE沿DE折起到△A1DE的位置，使AC⊥CD，如图2．