题目内容
若定义域为R的奇函数f(x)满足f(1+x)=-f(x),则下列结论:
①f(x)的图象过点(1,0);
②f(x)的图象关于直线x=
对称;
③f(x)是周期函数,且2是它的一个周期;
④f(x)在区间(-1,1)上是单调函数.
其中正确结论的序号是 .
①f(x)的图象过点(1,0);
②f(x)的图象关于直线x=
| 1 |
| 2 |
③f(x)是周期函数,且2是它的一个周期;
④f(x)在区间(-1,1)上是单调函数.
其中正确结论的序号是
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:①由奇函数f(0)=0可判断,②由奇函数的性质和对称性的结论可判断;③由f(1+x)=-f(x)和周期性的定义可求出函数的周期;④根据函数的对称轴可作出判断
解答:
解:∵定义域为R的奇函数f(x)满足f(1+x)=-f(x),
∴f(1)=-f(0)=0,∴f(x)的图象过点(1,0),故①正确;
由f(1+x)=-f(x)=f(-x)得,f(x)的图象关于直线x=
对称,故②正确;
用x+1替换f(1+x)=-f(x)中的x可得f(x+2)=-f(x+1)=f(x),
∴f(x)是周期函数,且2是它的一个周期,故③正确;
∵f(x)的图象关于直线x=
对称,
∴f(x)在区间(-1,1)上不是单调函数,故④不正确;
故答案为;①②③.
∴f(1)=-f(0)=0,∴f(x)的图象过点(1,0),故①正确;
由f(1+x)=-f(x)=f(-x)得,f(x)的图象关于直线x=
| 1 |
| 2 |
用x+1替换f(1+x)=-f(x)中的x可得f(x+2)=-f(x+1)=f(x),
∴f(x)是周期函数,且2是它的一个周期,故③正确;
∵f(x)的图象关于直线x=
| 1 |
| 2 |
∴f(x)在区间(-1,1)上不是单调函数,故④不正确;
故答案为;①②③.
点评:本题考查函数的性质,熟练掌握函数奇偶性、周期性、对称性的定义是解决问题的关键,属基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
设i为虚数单位,则复数z=
在复平面对应的点位于( )
| 1-2i |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
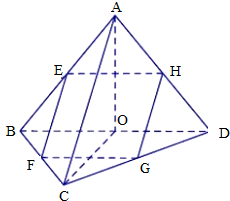 在三棱锥A-BCD中,点E、F、G、H分别是AB、BC、CD、DA的中点.
在三棱锥A-BCD中,点E、F、G、H分别是AB、BC、CD、DA的中点.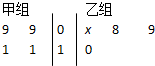 如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )
如图,茎叶图记录了甲、乙两组各四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.若甲、乙两组共有8名同学植树棵数的平均数为9,则x为( )