题目内容
定义在R上的函数f(x)既是偶函数又是周期函数.若f(x)的最小正周期是π,且当x∈[0,
]时,f(x)=sinx,则f(
)的值为( )
| π |
| 2 |
| 8π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:三角函数的周期性及其求法
专题:三角函数的求值
分析:要求f(
),则必须用f(x)=sinx来求解,那么必须通过奇偶性和周期性,将变量转化到区间[0,
]上,再应用其解析式求解.
| 8π |
| 3 |
| π |
| 2 |
解答:
解:∵f(x)的最小正周期是π
∴f(
)=f(
-3π)=f(-
)
∵函数f(x)是偶函数
∴f(
)=f(-
)=f(
)=sin
=
.
故选:C.
∴f(
| 8π |
| 3 |
| 8π |
| 3 |
| π |
| 3 |
∵函数f(x)是偶函数
∴f(
| 8π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故选:C.
点评:本题主要考查了函数的奇偶性,周期性以及应用区间上的解析性求函数值,是基础题,应熟练掌握.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
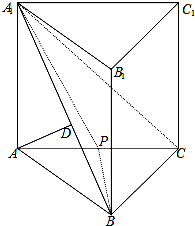 如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
如图,在直三棱柱ABC=A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.