题目内容
在△ABC中，若sinA：sinB：sinC=7：8：13，则△ABC中最大的内角是多少？
考点：正弦定理
专题：计算题,解三角形
分析：由已知及正弦定理可得a：b：c=7：8：13，令a=7k，b=8k，c=13k（k＞0），利用余弦定理有cosC=
=-
，可解得△ABC中最大的内角．
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
解答：
解：∵由正弦定理可得sinA：sinB：sinC=a：b：c，
∴a：b：c=7：8：13，
令a=7k，b=8k，c=13k（k＞0），
利用余弦定理有cosC=
=
=-
，
∵0°＜C＜180°，
∴C=120°．
∵c为最大边．
则△ABC中最大的内角是120°．
∴a：b：c=7：8：13，
令a=7k，b=8k，c=13k（k＞0），
利用余弦定理有cosC=
| a2+b2-c2 |
| 2ab |
| 49k2+64k2-169k2 |
| 112k2 |
| 1 |
| 2 |
∵0°＜C＜180°，
∴C=120°．
∵c为最大边．
则△ABC中最大的内角是120°．
点评：本题主要考察了正弦定理、余弦定理在解三角形中的应用，属于基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
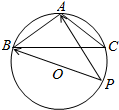如图，在△ABC中，三内角A，B，C的对边分别为a，b，c，且a2=b2+c2+bc，a=