题目内容
 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.(1)求二面角B-EC-A的正弦值;
(2)在线段BC上是否存在点F,使得E到平面PAF的距离为
2
| ||
| 5 |
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(1)由题意及正方形的特点,利用BC⊥AB,BC⊥PB得到BC⊥平面PAB,进而得到BC⊥PA,在利用CD⊥PA,得到线面垂直.过A作AH⊥BG于H,连接HE、AE,则∠AHE为二面角B-EC-A的平面角,求出AH,AE,即可求二面角B-EC-A的正弦值;
(2)设存在点F满足题意,过D作DM⊥AF于M,连PF,则DM⊥面APF,求出AF,可得BF,即可得出结论.
(2)设存在点F满足题意,过D作DM⊥AF于M,连PF,则DM⊥面APF,求出AF,可得BF,即可得出结论.
解答:
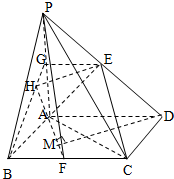 解.(1)取PA中点G,连接EG、BG,
解.(1)取PA中点G,连接EG、BG,
∵底面ABCD为正方形,
∴BC⊥AB,又BC⊥PB,
∴BC⊥平面PAB,
∴BC⊥PA.
同理CD⊥PA,
∴PA⊥平面ABCD.
过A作AH⊥BG于H,连接HE、AE.
∵BC⊥面PAB,∴AH⊥面GBCE
∵底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点
∴CE=
,AE=
,AC=2
,
∴AE⊥EC,
∴HE⊥EC
∴∠AHE为二面角B-EC-A的平面角,
∵AG=1,AB=2,
∴BG=
,
∴由等面积,可得AH=
=
,
∵AE=
∴在Rt△AHE中,sin∠AEH=
=
=
,
∴二面角B-EC-A的正弦值为
;
(2)设存在点F满足题意,过D作DM⊥AF于M,连PF,则DM⊥面APF.
∵E为PD为中点,E到面PAF距离为
∴DM=
,由平面几何知识知△DAM∽△AFB,求得AF=
∴BF=1,F为BC中点,
∴存在满足题意的点F.
 解.(1)取PA中点G,连接EG、BG,
解.(1)取PA中点G,连接EG、BG,∵底面ABCD为正方形,
∴BC⊥AB,又BC⊥PB,
∴BC⊥平面PAB,
∴BC⊥PA.
同理CD⊥PA,
∴PA⊥平面ABCD.
过A作AH⊥BG于H,连接HE、AE.
∵BC⊥面PAB,∴AH⊥面GBCE
∵底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点
∴CE=
| 6 |
| 2 |
| 2 |
∴AE⊥EC,
∴HE⊥EC
∴∠AHE为二面角B-EC-A的平面角,
∵AG=1,AB=2,
∴BG=
| 5 |
∴由等面积,可得AH=
| AB•AG |
| BG |
2
| ||
| 5 |
∵AE=
| 2 |
∴在Rt△AHE中,sin∠AEH=
| AH |
| AE |
| ||||
|
| ||
| 5 |
∴二面角B-EC-A的正弦值为
| ||
| 5 |
(2)设存在点F满足题意,过D作DM⊥AF于M,连PF,则DM⊥面APF.
∵E为PD为中点,E到面PAF距离为
2
| ||
| 5 |
∴DM=
4
| ||
| 5 |
| 5 |
∴BF=1,F为BC中点,
∴存在满足题意的点F.
点评:本题重点考查了线线垂直,线面垂直的判定与性质,考查了利用三垂线定理求解出二面角的平面角,考查学生的计算能力,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
若α,β是非零实数,则“α+β=0”是“|α|+|β|>0”成立的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
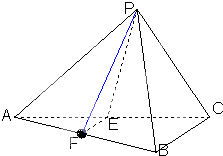 已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.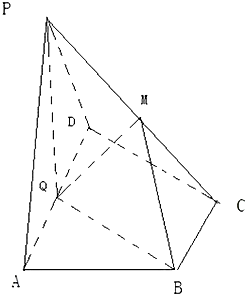 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=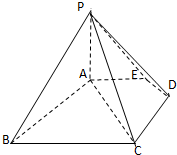 如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°,
如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°,