题目内容
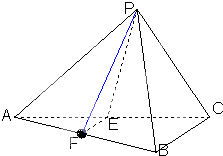 已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.(Ⅰ)证明PC⊥平面PAB;
(Ⅱ)求二面角P-AB-C的平面角的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定,与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离,空间角
分析:(I)连接CF,由△ABC,△PEF是正三角形且E,F为AC、AB的中点,可得PE=EF=
BC=
AC,可得PA⊥PC,进而可证明AB⊥面PCF,从而可得AB⊥PC,利用线面垂直的判定定理可证
(II)由AB⊥PF,AB⊥CF可得,∠PFC为所求的二面角,由(I)可得△PEF为直角三角形,Rt△PEF中,求解即可
| 1 |
| 2 |
| 1 |
| 2 |
(II)由AB⊥PF,AB⊥CF可得,∠PFC为所求的二面角,由(I)可得△PEF为直角三角形,Rt△PEF中,求解即可
解答:
 (Ⅰ)证明:连结CF.
(Ⅰ)证明:连结CF.
∵△ABC,△PEF是正三角形且E,F为AC、AB的中点,
∴PE=EF=
BC=
AC,
∴AP⊥PC.
∵CF⊥AB,PF⊥AB,CF∩PF=F,
∴AB⊥平面PCF.
∵PC?平面PCF,
∴PC⊥AB,
∵AB∩AP=A,
∴PC⊥平面PAB.
(Ⅱ)∵AB⊥PF,AB⊥CF,
∴∠PFC为所求二面角的平面角.
设AB=a,则AB=a,
Rt△PEF中,PF=EF=
,CF=
a.
∴cos∠PFC=
=
.
 (Ⅰ)证明:连结CF.
(Ⅰ)证明:连结CF.∵△ABC,△PEF是正三角形且E,F为AC、AB的中点,
∴PE=EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴AP⊥PC.
∵CF⊥AB,PF⊥AB,CF∩PF=F,
∴AB⊥平面PCF.
∵PC?平面PCF,
∴PC⊥AB,
∵AB∩AP=A,
∴PC⊥平面PAB.
(Ⅱ)∵AB⊥PF,AB⊥CF,
∴∠PFC为所求二面角的平面角.
设AB=a,则AB=a,
Rt△PEF中,PF=EF=
| a |
| 2 |
| ||
| 2 |
∴cos∠PFC=
| ||||
|
| ||
| 3 |
点评:本小题主要考查空间线面垂直的关系、二面角的度量等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO=
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO= 如图,斜三棱柱ABC-A1B1C1的侧棱长为
如图,斜三棱柱ABC-A1B1C1的侧棱长为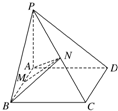 如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.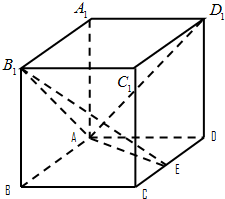 如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点. 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.