题目内容
求函数f（x）=x+
（p＞0为常数）在（0，+∞﹚上的单调区间．
| p |
| x |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：首先，求导数，然后，分别令导数大于零和小于零，直接求解单调区间即可．
解答：
解：∵f′（x）=1-
，
令f′（x）＞0，解得x＞
；
令f′（x）＜0，解得0＜x＜
，
所以，增区间为（
，+∞）：
减区间为：（0，
）．
| p |
| x2 |
令f′（x）＞0，解得x＞
| p |
令f′（x）＜0，解得0＜x＜
| p |
所以，增区间为（
| p |
减区间为：（0，
| p |
点评：本题重点考查了函数的导数与其单调性之间的关系，属于中档题．
练习册系列答案
相关题目
在△ABC中，若c=acosB，则△ABC中一定为（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等边三角形 |
| D、锐角三角形 |
已知点A（1，0）、B（2，0），点C在y轴的正半轴上，求∠ACB取最大值时，C点的坐标．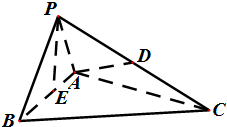
如图，四面体P-ABC中，△PAB为边长为1的等边三角形，△PBC与△PAC均为斜边为PC的直角三角形，且PC=
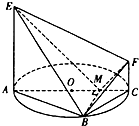如图，AC是圆O的直径，点B在圆O上，∠BAC=30°，BM⊥AC交AC于点M，EA⊥平面ABC，FC∥EA，AC=4，EA=3，FC=1．