题目内容
 已知点A(1,0)、B(2,0),点C在y轴的正半轴上,求∠ACB取最大值时,C点的坐标.
已知点A(1,0)、B(2,0),点C在y轴的正半轴上,求∠ACB取最大值时,C点的坐标.考点:余弦定理
专题:解三角形
分析:设OC=x,则AC,BC可用x表示,进而表示出cos∠ACB,利用基本不等式求得cos∠ACB取最大值时,x的值,则C的坐标可得.
解答:
解:设OC=x,则AC=
,BC=
,AB=1,
∴cos∠ACB=
=
=
,
∵x2+
≥4,当x2=2,即x=
时,取等号,
即当x=
时,cos∠ACB最大,
此时C的坐标为(0,
)
| 1+x2 |
| 4+x2 |
∴cos∠ACB=
| AC2+BC2-AB2 |
| 2AC•BC |
| 1+x2+4+x2-1 | ||||
2•
|
1+
|
∵x2+
| 4 |
| x2 |
| 2 |
即当x=
| 2 |
此时C的坐标为(0,
| 2 |
点评:本题主要考查了余弦定理的应用,基本不等式的性质.在运用基本不等式求最值时,注意“一正,二定,三相等”的条件的满足.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
cos(-
π)的值为( )
| 79 |
| 6 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
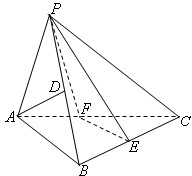 在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.
在三棱锥P-ABC中,已知PA=PB,∠ABC为直角,点D,E分别为PB,BC的中点.