题目内容
等差数列{an}中,a2=4,S6=42.
(1)求数列的通项公式an;
(2)设bn=
,Tn=b1+b2+…+bn,求T10.
(1)求数列的通项公式an;
(2)设bn=
| 2 |
| (n+1)an |
考点:数列的求和,等差数列的通项公式
专题:点列、递归数列与数学归纳法
分析:(1)根据条件联立方程,求出首项和公差,即可求数列的通项公式an;
(2)求出bn的通项公式,利用裂项法进行求和即可得到结论.
(2)求出bn的通项公式,利用裂项法进行求和即可得到结论.
解答:
解:(1)∵a2=4,S6=42,
∴
,解得d=2,a1=2,
则an=2n.
(2)∵bn=
=
-
,Tn=b1+b2+…+bn,
∴T10=
-
+
-
+…-
=
.
∴
|
则an=2n.
(2)∵bn=
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴T10=
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 11 |
| 10 |
| 11 |
点评:本题主要考查等差数列的通项公式以及数列求和,利用裂项法是解决本题的关键.

练习册系列答案
相关题目
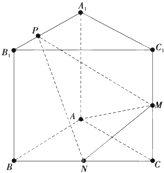 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且 如图,已知椭圆
如图,已知椭圆