题目内容
设等差数列{an}的前n项和为Sn，若a5=2，则2S6+S12=（ ）
| A、6 | B、12 | C、24 | D、48 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：数列{an}为等差数列，a5=2，可得a1+4d=2，利用等差数列的求和公式可得2S6+S12=2（6a1+15d）+（12a1+66d）=24（a1+4d），即可得出结论．
解答：
解：∵数列{an}为等差数列，a5=2，
∴a1+4d=2，
∴2S6+S12=2（6a1+15d）+（12a1+66d）=24（a1+4d）=48．
故选：D．
∴a1+4d=2，
∴2S6+S12=2（6a1+15d）+（12a1+66d）=24（a1+4d）=48．
故选：D．
点评：本题考查等差数列的通项公式的认识和理解，考查方程思想的运用，考查数列的前n项和和它的项之间的关系，注意运用项的之间的联系可以简化求解．
练习册系列答案
相关题目
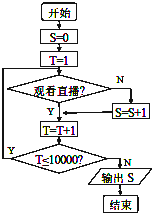为了解“伦敦奥运会开幕式”电视直播节目的收视情况，某机构在某地随机抽查了10000人，把抽查结果输入如图所示的程序框图中，其输出的数值是3700，则该节目的收视率为（ ）| A、3700 | B、630 |
| C、0.63 | D、0.37 |
由a1=1，d=3确定的等差数列{an}，当an=295时，序号n等于（ ）
| A、98 | B、99 | C、95 | D、100 |
X大学2014年自主招生报名刚结束，某考生想知道这次报考的人数，他随机记录了50个考生的考号；已知考生的考号是从0001，0002，0003，…这样从小到大依次顺序排列．经计算，这50个考号的和是24966（其中0001+0002视为3），据此，估计2014年参加X大学自主招生的考生数约为（ ）
| A、500人 | B、1000人 |
| C、1500人 | D、2000人 |
定积分
cosxdx=（ ）
| ∫ | π 0 |
| A、-1 | B、0 | C、1 | D、π |
已知集合A={y|y=-x2+1，x∈R}，B={y|y=2x，x∈R}则（ ）
| A、A⊆B |
| B、B⊆A |
| C、∁RA⊆B |
| D、B⊆∁RA |