题目内容
双曲线C1的中心在原点,焦点在x轴上,且过点A(
,
),双曲线C2中心在原点,焦点在y轴上,且过点B(
,
).C1的实轴长等于C2虚轴长,C1的虚轴长等于C2实轴长,求双曲线C1、C2的方程.
| 5 |
| 3 |
| 10 |
| 7 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:设C1:
-
=1,C2:
-
=1,由题意设a1=b2=a,a2=b1=b,则
-
=1,且
-
=1,由此能求出双曲线C1和C2的方程.
| x2 |
| a1 |
| y2 |
| b1 |
| y2 |
| a2 |
| x2 |
| b2 |
| 5 |
| a |
| 3 |
| b |
| 7 |
| b |
| 10 |
| a |
解答:
解:设C1:
-
=1,C2:
-
=1,
由题意设a1=b2=a,a2=b1=b,
∵双曲线C1的中心在原点,焦点在x轴上,且过点A(
,
),
∴
-
=1,①
∵双曲线C2中心在原点,焦点在y轴上,且过点B(
,
),
∴
-
=1,②
由①②解得a=
,b=
.
∴双曲线C1:2x2-3y2=1,双曲线C2:3y2-2x2=1.
| x2 |
| a1 |
| y2 |
| b1 |
| y2 |
| a2 |
| x2 |
| b2 |
由题意设a1=b2=a,a2=b1=b,
∵双曲线C1的中心在原点,焦点在x轴上,且过点A(
| 5 |
| 3 |
∴
| 5 |
| a |
| 3 |
| b |
∵双曲线C2中心在原点,焦点在y轴上,且过点B(
| 10 |
| 7 |
∴
| 7 |
| b |
| 10 |
| a |
由①②解得a=
| 1 |
| 2 |
| 1 |
| 3 |
∴双曲线C1:2x2-3y2=1,双曲线C2:3y2-2x2=1.
点评:本题考查双曲线方程的求法,是中档题,解题时要认真审题,注意双曲线的简单性质的灵活运用.

练习册系列答案
相关题目


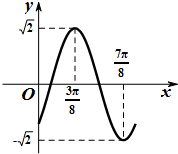 已知函数f(x)=asin(ωx+θ)的部分图象如下图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)的部分图象如下图,其中ω>0,|θ|<