题目内容
已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f′(x)g(x)>f(x)g′(x),且f(x)=axg(x)(a>0,且a≠1),
+
=
.若数列{
}的前n项和大于126,则n的最小值为( )
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 5 |
| 2 |
| f(n) |
| g(n) |
| A、6 | B、7 | C、8 | D、9 |
考点:导数的运算
专题:导数的概念及应用
分析:令h(x)=
,由题意可知a>1,由
+
=a+
=
.求出a=2,由此可知Sn的表达式,前n项和大于126,求出n的最小值.
| f(x) |
| g(x) |
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 1 |
| a |
| 5 |
| 2 |
解答:
解:令h(x)=
则h′(x)=
>0,
故h(x)=ax单调递增,
所以a>1,
又
+
=a+
=
.
解得a=2,
则
=2n,
其前n项和Sn=2n-1
由2n-1>126,
得n≥7.
故选:B
| f(x) |
| g(x) |
则h′(x)=
| f′(x)g(x)-f(x)g′(x) |
| g2(x) |
故h(x)=ax单调递增,
所以a>1,
又
| f(1) |
| g(1) |
| f(-1) |
| g(-1) |
| 1 |
| a |
| 5 |
| 2 |
解得a=2,
则
| f(n) |
| g(n) |
其前n项和Sn=2n-1
由2n-1>126,
得n≥7.
故选:B
点评:本题考查概率的求法和导数的性质,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答,注意概率计算公式的灵活运用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
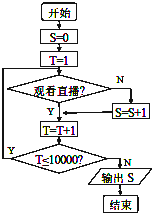 为了解“伦敦奥运会开幕式”电视直播节目的收视情况,某机构在某地随机抽查了10000人,把抽查结果输入如图所示的程序框图中,其输出的数值是3700,则该节目的收视率为( )
为了解“伦敦奥运会开幕式”电视直播节目的收视情况,某机构在某地随机抽查了10000人,把抽查结果输入如图所示的程序框图中,其输出的数值是3700,则该节目的收视率为( )| A、3700 | B、630 |
| C、0.63 | D、0.37 |
已知集合A={y|y=-x2+1,x∈R},B={y|y=2x,x∈R}则( )
| A、A⊆B |
| B、B⊆A |
| C、∁RA⊆B |
| D、B⊆∁RA |
函数f(x)=x-1的零点是( )
| A、0 | B、1 |
| C、(0,0) | D、(1,0) |
若关于x的不等式(x2-1)•(x-a)<0没有正整数解,则实数a的最大值为( )
| A、3 | B、2 | C、1 | D、0 |