Question

如图，正四棱柱ABCD-A′B′C′D′中，底面边长为2，侧棱长为3，E为BC的中点，FG分别为CC′、DD′上的点，且CF=2GD=2．求：
（1）C′到面EFG的距离；
（2）DA与面EFG所成的角；
（3）在直线BB′上是否存在点P，使得DP∥面EFG？，若存在，找出点P的位置，若不存在，试说明理由．

Answer 1

考点：点、线、面间的距离计算,直线与平面平行的判定,直线与平面所成的角

专题：综合题,空间位置关系与距离,空间角

分析：（1）以D为原点建立空间直角坐标系，并求出面EFG的一个法向量

n

，及面EFG上任一点与C′连线的方向向量，代入公式d=

| n • C′F |

| n |

中，即得到C′到面EFG的距离；
（2）求出DA的方向向量，结合（1）中所求的面EFG的法向量

n

的坐标，代入向量夹角公式，即可得到DA与面EFG所成的角的正弦值；
（3）设出P点坐标，求出DP的方向向量，根据DP∥面EFG，则

DP

•

n

=0，可以构造关于P点坐标的方程组，解方程组，即可得P点坐标．

解答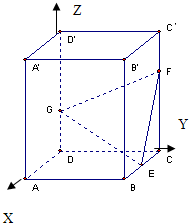： 解：如图，以D为原点建立空间直角坐标系，则E（1，2，0），F（0，2，2），G（0，0，1）
∴

EF

=（-1，0，2），

FG

=（0，-2，-1），
设

n

=（x，y，z）为面EFG的法向量，则

x=2z z=-2y

，取y=1，
得

n

=（-4，1，-2）…（4分）
（1）∵

C′F

=（0，0，-1），
∴C’到面EFG的距离为d=

| n • C′F |

| n |

=

2 21

21

…（6分）
（2）

DA

=（2，0，0），设DA与面EFG所成的角为θ，
则sinθ=

| DA • n |

| DA || n |

=

4 21

21

．   …（10分）
（3）存在点P，在B点下方且BP=3，此时P（2，2，-3），

DP

=（2，2，-3），
∴

DP

•

n

=0，∴DP∥面EFG．…（14分）

点评：本题考查的知识点是用空间向量求直线与平面的夹角，直线与平面平行的判定，点到平面的距离计算，其中由于三个小题的结论均与面EFG有关，故求出平面EFG的法向量是解答本题的关键．