题目内容
已知不等式ax2+bx-2>0的解集是{x|-2<x<-
},则a-b的值为( )
| 1 |
| 4 |
| A、2 | B、3 | C、4 | D、5 |
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:由不等式ax2+bx-2>0的解集是{x|-2<x<-
},可得-2,-
是一元二次方程ax2+bx-2=0的两个实数根,利用根与系数的关系即可得出.
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:∵不等式ax2+bx-2>0的解集是{x|-2<x<-
},
∴-2,-
是一元二次方程ax2+bx-2=0的两个实数根,
∴-2-
=-
,-2×(-
)=-
,
解得a=-4,b=-9.
∴a-b=5.
故选:D.
| 1 |
| 4 |
∴-2,-
| 1 |
| 4 |
∴-2-
| 1 |
| 4 |
| b |
| a |
| 1 |
| 4 |
| 2 |
| a |
解得a=-4,b=-9.
∴a-b=5.
故选:D.
点评:本题考查了一元二次不等式的解集与相应的一元二次方程的实数根的关系,考查了计算能力,属于基础题.

练习册系列答案
相关题目
以双曲线
-
=1的右顶点为焦点的抛物线的标准方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
| A、y2=4x |
| B、y2=16x |
| C、y2=8x |
| D、y2=-8x |
设△ABC的内角A,B,C所对的边分别为a,b,c.若(a+b-c)(a+b+c)=ab,则角C=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
| B、命题“?x≥0,x2+x-1<0”的否定是“?x0<0,x02+x0-1≥0” |
| C、命题“若x=y,则sin x=sin y”的逆否命题为假命题 |
| D、若“p∨q”为真命题,则p,q中至少有一个为真命题 |
若椭圆
+y2=1与双曲线
-
=1 (a>0)有相同的焦点,则a=( )
| x2 |
| 4 |
| x2 |
| a2 |
| y2 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
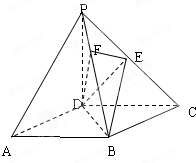 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB于点F.