题目内容

14．椭圆4x2+9y2=144内有一点P（3，2），则以P为中点的弦所在直线的斜率为（　　）
A．$-\frac{2}{3}$B．$-\frac{3}{2}$C．$-\frac{4}{9}$D．$-\frac{9}{4}$

分析 利用中点坐标公式、斜率计算公式、“点差法”即可得出．

解答 解：设以点P为中点的弦所在直线与椭圆相交于点A（x1，y1），B（x2，y2），斜率为k．
则$4{{x}_{1}}^{2}+9{{y}_{1}}^{2}=144$，$4{{x}_{2}}^{2}+9{{y}_{2}}^{2}=144$，两式相减得4（x1+x2）（x1-x2）+9（y1+y2）（y1-y2）=0，
又x1+x2=6，y1+y2=4，$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=k，
代入解得k=-$\frac{4}{9}×\frac{6}{4}$=$-\frac{2}{3}$．
故选：A．

点评 熟练掌握中点坐标公式、斜率计算公式、“点差法”是解题的关键．

练习册系列答案
相关题目
4．若tanα=3tan$\frac{π}{5}$，则$\frac{cos（α-\frac{3π}{10}）}{sin（α-\frac{π}{5}）}$=（　　）
A．1B．2C．3D．4
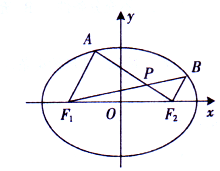5．设F1，F2是椭圆C：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），的左右焦点，离心率为$\frac{\sqrt{2}}{2}$，M为椭圆上的动点，|MF1|的最大值为1$+\sqrt{2}$．
（Ⅰ）求椭圆C的方程．
（Ⅱ）设A，B是椭圆上位于x轴上方的两点，且直线AF1与直线BF2平行，AF2与BF1交于点P，求证：|PF1|+|PF2|是定值．
2．已知函数f（x）=g（x）+x2，对于任意x∈R总有f（-x）+f（x）=0，且g（-1）=1，则g（1）=（　　）
A．-1B．1C．3D．-3
9．设抛物线E：y2=2px（p＞0）上的点M（x0，4）到焦点F的距离|MF|=$\frac{5}{4}$x0．
（Ⅰ）求抛物线E的方程；
（Ⅱ）如图，直线l：y=k（x+2）与抛物线E交于A，B两点，点A关于x轴的对称点是C，求证：直线BC恒过一定点．
19．设F1，F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{2a}=1（{a＞0}）$的两个焦点，点M在双曲线上，且满足$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}=0$，$|{\overrightarrow{M{F_1}}}|•|{\overrightarrow{M{F_2}}}|=4$，则a的值等于1．
6．已知函数$f（x）=cos2xcosθ-sin2xcos（{\frac{π}{2}-θ}）（{|θ|＜\frac{π}{2}}）$在$（{-\frac{3π}{8}，-\frac{π}{6}}）$上单调递增，则$f（{\frac{π}{16}}）$的最大值为1．
3．已知函数f（x）=$\frac{a•{2}^{x}+b+1}{{2}^{x}+1}$是定义域在R上的奇函数，且f（2）=$\frac{6}{5}$．
（1）求实数a、b的值；
（2）判断函数f（x）的单调性，并用定义证明；
（3）解不等式：f（log${\;}_{\frac{1}{2}}$（2x-2）]+f[log2（1-$\frac{1}{2}$x）]≥0．
4．已知集合A={0，2，4，6}，B={x∈N|2x＜33}，则集合A∩B的子集个数为（　　）
A．8B．7C．6D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网